Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M4N06, AC9M4N07
Numeracy Progression: Number and place value: P7, Additive strategies: P8, Multiplicative strategies: P7
At this level, students develop efficient strategies and use appropriate digital tools for solving problems involving addition and subtraction, and multiplication and division where there is no remainder. They use estimation and rounding to check and explain the reasonableness of calculations.
To build relational understanding of multiplication tables, provide students with opportunities to represent the product of numbers using concrete, symbolic and visual representations. This will help them appreciate the magnitude of number facts and make connections between related facts and the inverse division facts.
Build in the process of estimation, for example, using rounding when making calculations. Encourage students to use this to check the reasonableness of their calculations and as a useful self-check step.
Use manipulatives to reinforce the big ideas of multiplication and division. For example, a digital hundreds chart will help students recognise times table patterns and students see the link between additive and multiplicative thinking. Display array representations and ask students to describe their structure.
Use questioning and feedback to help students articulate and develop big ideas such as commutativity or the inverse relationship between multiplication and division to further support students’ multiplicative reasoning.
Teaching and learning summary:
- Make explicit the multiplicative relationships of our place value system.
- Model ways to solve problems involving multiplication and division, using materials, arrays, repeated addition, mental methods, and multiplication and division facts, including problems in contexts.
- Establish a culture of incorporating estimation as a self-checking process when undertaking calculations.
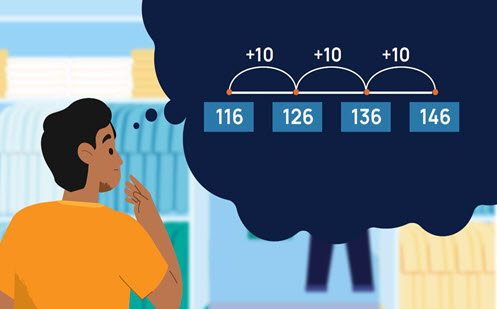
Students:
- use relevant strategies to solve addition and subtraction problems
- recall and use multiplication and division facts using strategies such as doubling and halving, jump strategies, place value partitioning and compensation
- use written and visual representations such as arrays and bar models to solve simple multiplication and division problems
- describe commutativity, inverse relationships and multiplication as repeated addition.
Some students may:
- rely on rote learning or a naive ‘groups of’ understanding for multiplication, based on repeated addition. Arrays and regions support the shift from an additive ‘groups of’ model to a factor-factor-product model. This is needed to support fraction representation, the multiplication and division of larger whole numbers, fractions and decimals, and algebra.
- not yet to understand the inverse relationship between multiplication and division. They find it a challenge to move beyond thinking of division as sharing and require support to also think of division as grouping.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning to practise and develop our multiplication and division skills through the game Four go.
Why are we learning about this?
- This game gives us the opportunity to estimate answers to calculations in a fun way, and gives plenty of practice in multiplication and division.
What to do
- You are going to play the game Four go with a family member or friend.
- Follow the instructions for setting up your game board.
- Play the game a few times. See if you can develop a winning strategy.
Success criteria
I can:
- solve multiplication and division facts and explain my thinking.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Concrete, Representational, Abstract (CRA model)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -
Classroom talks
Classroom talks enable students to develop language, build mathematical thinking skills and create mathematical meaning through collaborative conversations.
Go to resource -
Feedback
It has been shown that good feedback can make a significant difference to a student’s future performance.
Go to resource -
Differentiated teaching
Differentiation involves teachers creating lessons that are accessible and challenging for all students.
Go to resource -

Worked examples
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

It is odd – or is it?
In this lesson, students investigate the properties of odd and even numbers.
Go to resource -

Pocket money: Saving for an item
In this lesson students use efficient strategies when performing calculations involving money.
Go to resource -

Pocket money: Partitioning money amounts
In this lesson students create an infographic to communicate their findings from their statistical investigation.
Go to resource -
Developing flowcharts: Halving strategy
In this lesson, students create a flowchart outlining the sequence of steps required when using the halving strategy for division.
Go to resource -
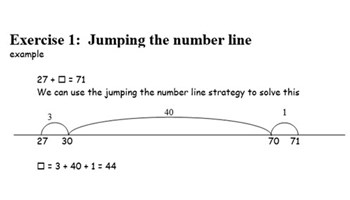
Addition and subtraction strategies
Use this guide to provide tasks to practise number properties and strategies for addition and subtraction.
Go to resource -

Tables teaser
Students use this interactive tool to think in 'reverse' – the answers to the multiplication calculations are given, and students need to choose the appropriate times tables facts.
Go to resource -
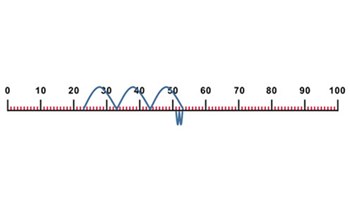
Five steps to 50
Use this task to practise jump strategy for addition using 50 as landmark number.
Go to resource -
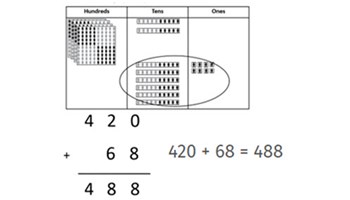
Addition with hundreds and tens
Use this lesson this to support students to solve addition problems using place value parts.
Go to resource -

Anticipating the result of equal subtraction (quotative division)
Use this lesson to support students to use their knowledge of addition and multiplication basic facts to anticipate the result of equal subtraction situations.
Go to resource -
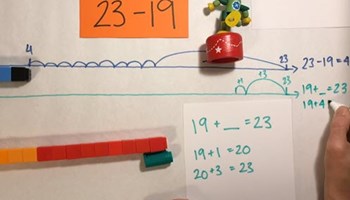
Let’s talk 1: Stage 2
In this video, students are asked to think of five different strategies to solve the problem, 23 – 19.
Go to resource -
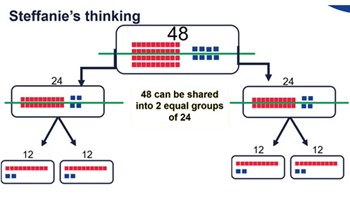
Let's talk: How many ways?
Use this video to discuss strategies to solve problems using multiplicative thinking.
Go to resource -

Deriving facts by doubling
The purpose of this activity is to support students to recognise that scaling applies to comparisons where one amount is less than another.
Go to resource -

Additive strategies: Video and teaching guide
Use this video to explore the use of computation strategies, rounding and estimation in real-world, additive situations.
Go to resource -
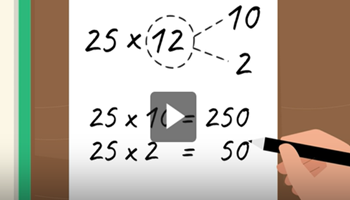
Multiplication: 2 digit by 2 digit numbers
Use this video and teaching guide to explore multiplicative strategies, methods and models to solve a given worded problem.
Go to resource -
Number relations
This unit of work investigates how relational thinking is applied to number operations.
Go to resource
Assessment
By the end of Year 4, students use their proficiency with addition and multiplication facts to add and subtract, and multiply and divide numbers efficiently. They choose rounding and estimation strategies to determine whether results of calculations are reasonable.
-
Assessment: Finding factors
Use this task to find out if students understand and can use the inverse relationship between multiplication and division.
Go to resource -

Assessment: Calculator number sentences
Use this task to find out if students can choose the appropriate operation to solve a wide range of multiplication and divisions problems with a calculator.
Go to resource -

Number: addition and subtraction
Use this task to assess students’ proficiency in addition and subtraction.
Go to resource