Multiplication: 2 digit by 2 digit numbers: Video and teaching guide
Use this video to explore multiplicative strategies, methods and models to solve a given worded problem.
The video uses the scenario of a student helping her younger brother with a maths problem. They explore and discuss methods for solving the problem: ‘How many months has a 25 year old been alive?’
We show how prior knowledge is required to know what type of calculation to perform, before exploring and discussing different multiplication strategies that use partitioning. Area model, box model and vertical algorithm methods are then demonstrated.
Watch the video below with your students (full screen recommended).
Video duration: 3 min 56 sec
Suggestions to follow up video
Begin with reasoning
Objective: To understand the important role reasoning plays at the start of solving a worded problem in determining what calculation is required.
In the video, the older sister helps her younger brother to solve a maths problem. The older sister models her method by stating what she already knows to help determine the calculation they will need to make in order to solve the problem: How many months has a 25 year old been alive?
Older sister: A person who is one year old has lived for 12 months. So, when they are 25, they have lived…
Young brother: …so to work it out, it’s 25 x 12.
Stating the problem out loud, and stating out loud what we know about the situation (for example, the number of months in a year), is a powerful way to help us know what calculation we need to make.

Role of teacher: Make explicit the importance of reasoning at the start when approaching worded problems. Provide frequent opportunities to practise reasoning aloud why we are convinced that a particular calculation will give us the answer required for the question being asked.
Partitioning (using partial products)
Objective: To understand that breaking up one or both numbers (use partial products) can sometimes help make a multiplication problem easier to solve.
In the video, the older sister uses recording to demonstrate two methods with grounding in the distributive property.
First, she solves 25 x 12 by breaking 12 (the multiplier) into two parts: 10 and 2. She demonstrates that 25 x 12 is the same as (25 x 10) + (25 x 2) and uses these facts to solve the problem.
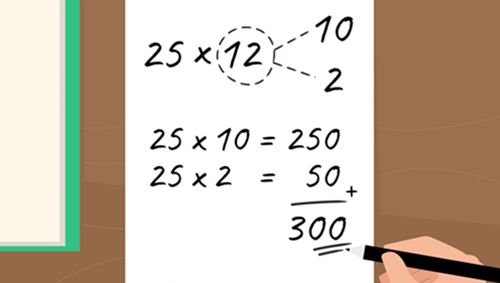
She then demonstrates how a solution might look when breaking both numbers (25 and 12) into partial products, for example, 25 x 12 = (20 + 5) x (10 +2)
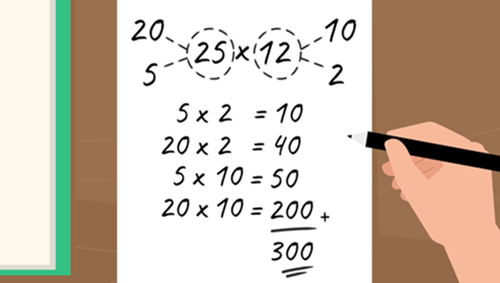
Questions for students to consider/explore:
- How are these two methods the same?
- How are these two methods different?
- Which is your preferred of the two, and why?
How else could one or both numbers be manipulated to make the problem easier?
Role of teacher: Ensure a safe space where students have time to consider and make sense of the strategies presented. Help students see that by thinking about the numbers involved in a calculation, we can often use what we know about numbers to make the calculation easier.
The area model
Objective: To understand that the area model is a proportional model that can help us to see how and why partitioning works when multiplying larger numbers.
This model represents a second partitioning method: 25 x 12 = (20 + 5) x (10 +2).
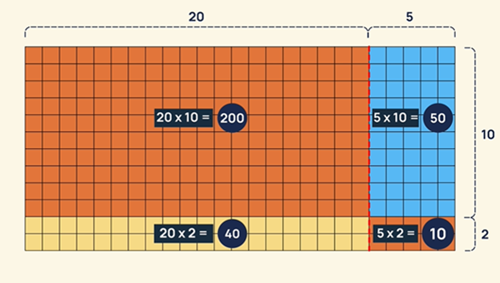
Questions for students to consider/explore:
- What do you notice and wonder about this area model?
- How does this model make sense to you?
- What connections can be made between this visual model and the vertical algorithm method shown toward the end of the video?

Role of teacher: Ensure students understand that the area model is a proportional model, where the actual size of each part is represented. Encourage students to reason how and why the area model shown is an accurate representation.
Help students see the value of area models for understanding how and why multiplication works, as well as for visualising the relationship between multiplication and division.
The box model
Objective: To understand that the box model is a non-proportional model that can help us to see how and why partitioning works when multiplying larger numbers.
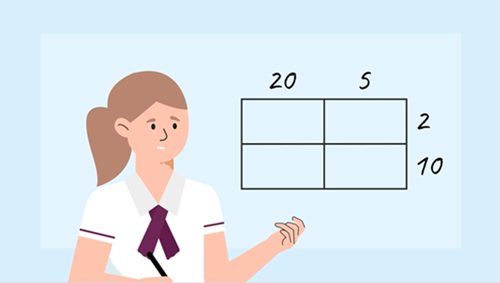
Role of teacher: Ensure students understand that the box model is a non-proportional model; it doesn’t show the size difference between parts. Encourage students to reason how and why the box model shown is a useful representation.
One problem, multiple solutions
Objective: To understand that many multiplication problems (like 25 x 12) have multiple ways to solve them. Know that while there is no ‘one right way’ to solve a problem, there may be a particular method or two that you prefer to use.
In the video, we see a number of different ways to solve 25 x 12.
Questions for students to consider/explore:
- What other ways can 25 x 12 be manipulated to help solve the problem?
- What if 25 only was broken into parts? How might a solution look?
- How might doubling one number and halving the other help? For example, double 25 and halve 12: 25 x 12 = 50 x 6 = 300. How and why does the doubling/halving strategy work?
- Of the different strategies you explored (including those in the video), consider which you prefer, and why?

Role of teacher: Make explicit the benefits of exploring and thinking about different solutions to multiplication problems. Benefits can include:
- understanding how and why strategies (such as partitioning) work will help us develop other skills and understandings in other areas more easily (such as in algebra)
- gaining new perspectives and discovering strategies that we may find to be more efficient than those we are already using
- creating habits of mathematical reasoning, which ultimately support mathematical precision.