Springboard maths concepts
These videos cover a range of mathematical concepts and are intended to demonstrate maths used in everyday situations.
Use these videos with supporting teacher guides as a springboard to explore mathematical concepts.
The teacher guide highlights the key concepts of each video with suggestions on how to follow up in the classroom.
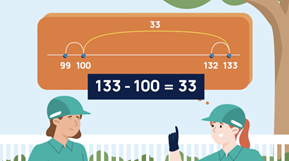
Additive strategies: Years 2–4
Use this video and teaching guide to explore the use of computation strategies, rounding and estimation in real-world, additive situations.

Multiplication: 2 digit by 2 digit numbers: Years 4–5
Use this video and teaching guide to explore multiplicative strategies, methods and models to solve a given worded problem.

Area and perimeter: Years 4–6
Use this video and teaching guide to explore concepts of area and perimeter, and connect these ideas to real-world situations.

Decimal fractions: Years 4–6
Use this video and teaching guide to explore decimal fractions, how they are represented and how we use them in day-to-day contexts.

Fractions as division: Years 5–6
Use this video and teaching guide as a springboard to explore multiplicative thinking using fractions, and to apply that thinking to sharing anything when there is not a whole number answer, drawing on reasoning.

Algebra basics: Years 6–7
Use this video and teaching guide as a springboard to introduce algebraic thinking, and to apply that thinking to a financial context, drawing on reasoning.
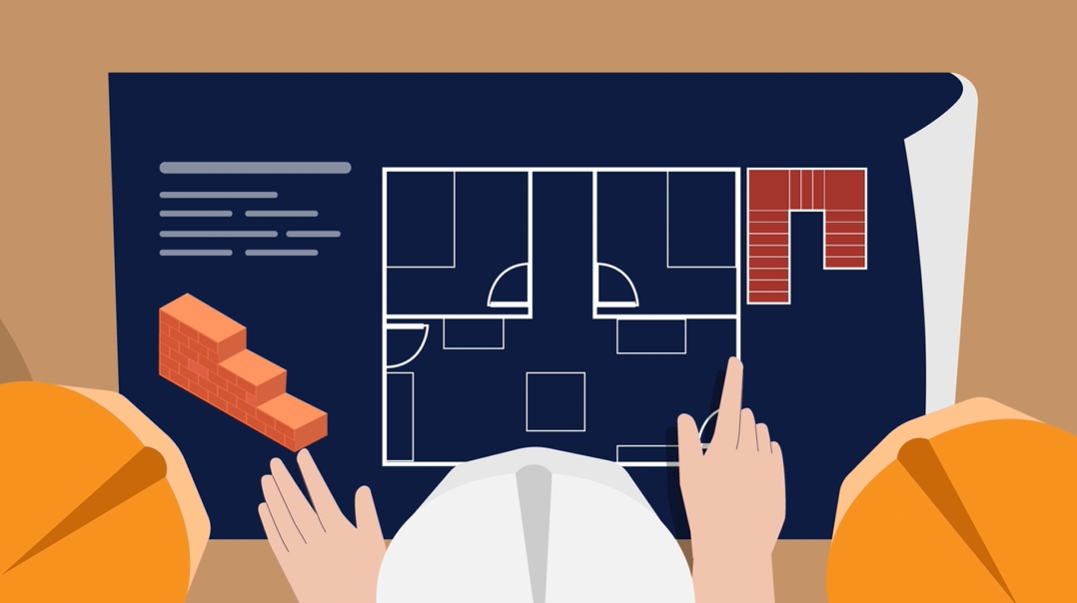
Volume and modelling: Year 7
Use this video and teaching guide as a springboard to explore volume of composite shapes, adjusting numbers to make calculations friendlier, and drawing on reasoning and mathematical modelling.

Algebraic equations: Years 7–8
Use this video and teaching guide as a springboard to explore algebraic thinking, and to apply that thinking to a financial context, drawing on reasoning and mathematical modelling.

Proportional reasoning: Years 7–8
Use this video and teaching guide as a springboard to explore scaling or proportional thinking, and to apply that thinking to a food-related context, drawing on reasoning and mathematical modelling.