Volume and modelling: Video and teaching guide

Use this video as a springboard to explore volume of composite shapes, adjusting numbers to make calculations friendlier, and drawing on reasoning and mathematical modelling.

The video uses the scenario of a project manager asking the construction team if there are enough bricks onsite to build three identical foundations. To determine if more bricks need to be ordered, the calculated number of bricks is then compared to the number available on the pallet.

Australian Curriculum V9 Mathematics
Year 7: Measurement
AC9M7M02, AC9M7M06

Numeracy Progression
Multiplicative Strategies: P7
Understanding units of measurement: P8, P9

*P stands for Progression level

Watch the video below with your students (full screen recommended).

Video duration: 3 min 19 sec

Suggestions to follow up video

Objective: To create different arrangements of blocks for a specified volume.

In this video, students will be shown strategies to calculate arrangements of bricks (rectangular prisms). You may decide to have students use cubes or blocks or isometric paper to create arrangements that are made up of a set number. For example, students might make an arrangement that has a volume of 24 blocks.

Role of teacher: Make explicit that there are multiple ways to arrange the blocks to make a volume of 24 blocks. These include: 2 wide x 3 long x 4 high; 1 wide x 24 long x 1 high; or 3 wide x 4 long x 2 high. Some students may be familiar with fact that the formula to calculate the volume of a rectangular prism is length x width x height.

Objective: To calculate the volume of stacked bricks in various arrangements, some of which cannot be seen.

Role of teacher: Make explicit that there is not one correct way to calculate the volume of bricks in various arrangements that are made up of composite shapes. We can use spatial visualisation to ‘see’ the composite shapes in different ways. If needed, use cubes to model the scenario in class.

In the video, the first task for Mindy and Raff is to calculate the number of bricks needed for the three foundations. Two methods of calculating the volume of the arrangement, some of which cannot be seen, are shown. Take time to explore the two strategies and have students talk about their preferred way to calculate the volume. They may suggest an alternative approach. Note that we are using informal units rather than formal units of cubic metres or cubic centimetres.

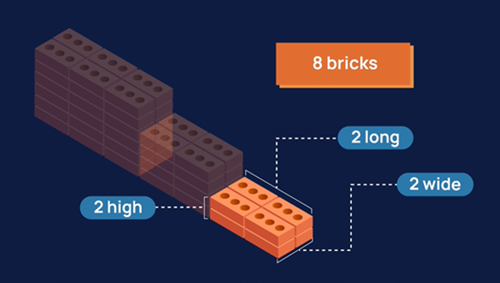
A diagram of a structure made of increasingly larger piles of bricks.

A diagram of a structure made of bricks. The structure is made up of three rectangular blocks, becoming increasingly larger. A block of 8 bricks in a rectangular shape at the fore is highlighted. Labels are shown 2 high, 2 long and 2 wide. Text in a box shows the volume of the highlighted section as 8 bricks.

Person wearing a hard hat and overalls looking at a structure made of bricks.

Person wearing a hard hat and overalls looking at a structure made of bricks. The brick structure is labelled in three parts: 1, the lowest part, which is made up of two rows of 6 bricks; 2, the middle part, which is made up of two rows of 5 bricks; and 3, the top section, which is made up of two rows of 3 bricks. Text in a box says ‘Splits the foundations into 3 layers of blocks’.

The next part of their task is to work out the total number of bricks needed. They do this by working out the number of bricks needed for one foundation and then multiplying by 3. This number is then compared to the bricks available onsite to decide if they have enough bricks.  

Discuss Mindy’s method of estimating the number of bricks in the stack and explore how she came up with 175 bricks. How do they check the estimate and then come up with an exact number of bricks?

Person wearing a hard hat and overalls near a pallet of bricks

Person wearing a hard hat and overalls near a pallet of bricks. The full pallet of bricks is made up of 8 layers in height, 4 bricks long and 6 bricks wide. A single column of bricks that is 8 high is labelled with an 8.

A possible strategy to estimate if there are enough bricks on the pallet is to use a number that is more friendly for the student and simpler to use. The pallet is made up of layers of 24 bricks. However, using 25 in the estimation is a more friendly number to multiply, 4 x 25 = 100 for four rows; 8 x 25 = 200 for 8 rows. As there are only 7 rows subtract 25 to get 175 bricks for the seven layers.

A calculation is used to determine the number of bricks against the estimate. In this example, Mindy breaks 24 into place value parts of 20 + 4, and then multiplies by 7. She then takes away the 5 bricks for the layer that was incomplete to get 168.

Ask students to share why they preferred a particular method for calculating the number of bricks – seeing other people’s methods may encourage them to expand their own thinking.

Explore options such as continuing the pattern as a growing pattern, reflection of original design, or any other pattern.

Objective: To devise a strategy to work out how much Raff and Mindy should charge for their work.

Role of teacher: Set the problem and avoid providing students with too much scaffolding. They may need to make assumptions or find out costs of laying bricks. The focus of this open-ended task is to apply problem-solving skills to come up with a suitable strategy.

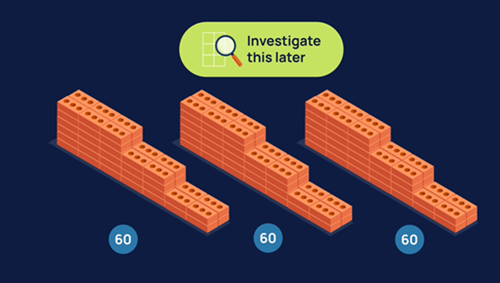
A diagram of three brick structures.

A diagram of three brick structures. Each structure is labelled with the number 60. Above the structures a text box includes a magnifying glass icon and says ‘Investigate this later’.

Ask students to reflect on their investigations related to volume and think about how they counted the total number of bricks needed and bricks available. When all the groups are the same size, using multiplication gives us an alternative – and is more efficient – than using repeated addition.

What makes a number friendly to you? Explain your thinking, perhaps with some examples.