Fractions as division: Video and teaching guide

Use this video as a springboard to explore multiplicative thinking using fractions, and to apply that thinking to sharing anything when there is not a whole number answer, drawing on reasoning.

The video uses the scenario of friends sharing food where the number of pieces does not share equally without remainders for the number of people or each person not receiving a whole portion. We show how to develop the idea of sharing as a strategy for division.

Australian Curriculum V9 Mathematics
Years 5–6: Number
AC9M5N07, AC9M6N07

Numeracy Progression
Interpreting fractions: P7, P8
Multiplicative Strategies: P7, P9

*P stands for Progression level

Watch the video below with your students (full screen recommended).

Video duration: 3 min 17 sec

Suggestions to follow up video

Objective: To understand that when there are more people to share between than items, this results in everybody receiving less than a whole item.

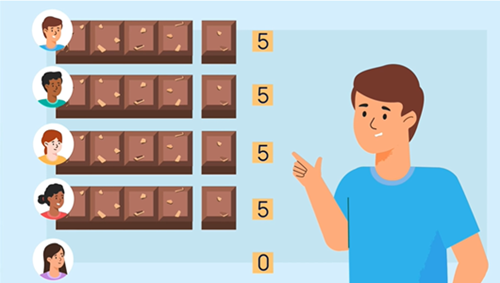
In the video, some friends are in a dilemma. There are four snack bars to share between five friends. Two ways of describing 4 ÷ 5 are explained. This means that either each whole bar could be divided equally into five pieces and then shared between the four friends. Alternatively, a piece is taken off each bar to give to the fifth friend so that they all receive the same amount.

Child thinking about a division problem.

Child thinking about a division problem. His thought bubble shows two rows, one is 4 chocolate bars, and underneath in the second row there are 5 people. The four chocolate bars are to be divided between the 5 people.

Role of teacher: Make explicit that this is about equal or fair sharing and not repeated subtraction. The type of division depends on whether the unknown amount is the number of groups or the size of the group. Repeated subtraction is when the amount each group receives is known and we subtract until there is nothing left. When the number of groups are known (in this case, how many friends) we are asking how much is in each group, which is sharing equally until the need to break into smaller pieces is reached. The reducing of piece size is repeated until there is nothing is left to share. Fair sharing can be done by either breaking each bar into the required number of pieces so each person receives 4 pieces the size of one-fifth, or a piece the size of one-fifth can be taken off each bar and given to the fifth person. If all the bars are the same flavour, which way the sharing is done won’t make a difference but if each bar is a different flavour and each person wants to have a piece of each flavour, then the first way of sharing must be done. Ask which way students would choose to share, and why.

Notice that the answer is in the question: 4 ÷ 5 = 45

Child pointing to 5 squares of chocolate.

Child pointing to 5 squares of chocolate. Text says 5 pcs (pieces) multiplied by 4, and underneath the equation, four chocolate bars are shown.

Child pointing to four chocolate bars and faces of five people.

Child showing how to divide 4 chocolate bars between 5 people. Along the left side are the faces of five students. Alongside each of the first four students is a chocolate bar, containing 5 squares of chocolate divided into a block of four and a single block. The number 5 is next to each chocolate bar. The fifth person has no chocolate, and a zero is shown as the chocolate tally for this person.

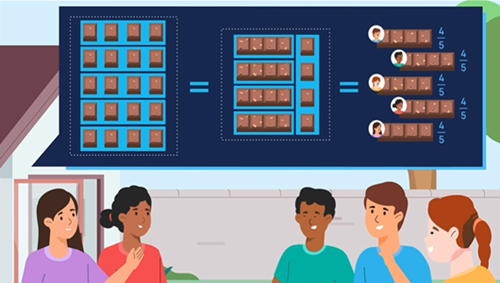
Five students showing how to share the 4 bars of chocolate equally.

Five students across bottom of image with box above them showing how to divide 4 chocolate bars between 5 people. There are five rows of chocolate each containing 4 squares of chocolate Next to a small image of each child is a row of four chocolate squares. Next to each row is the fraction four-fifths.

Objective: To understand that when there are fewer people to share between than items to be shared, this results in everybody receiving more than a whole item.

Four students in a lolly shop, with question text above them saying How can 10 licorice straps be shared equally here?

Four students in a lolly shop, with question text above them saying How can 10 licorice straps be shared equally here? No answer is given.

Role of teacher:

Make explicit that this is about sharing fairly or equally when there is more than enough to give each person a whole item. Demonstrate two ways of describing how 10 items could be shared equally between 4 friends. The first example is to divide each whole equally into two pieces, making 20 pieces in total, which can then be shared equally between the four friends. Alternatively, each person is given as many wholes as possible until the remaining pieces have to be made smaller, so that they all receive the same amount. Ask which way students would choose to share, and why.

Child showing how to share.

Child showing how to equally share 10 straps of licorice between four students. Four children are shown. Each person has 5 halves of a licorice strap. The number 5 is shown next to each.

Child showing how to share.

Child showing how to share licorice 10 straps licorice equally between four children. Each person has 2 and a half licorice straps. The number 2 and ½ is shown next to each person.

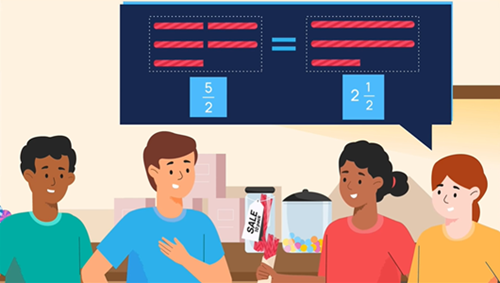
Four students in a lolly shop.

Four students in a lolly shop. Above them in a box is an image showing 5 halves of a licorice strap is equal to 2 and a half licorice straps. Under each image are the corresponding numbers 5/2 and 2 ½.

Notice again that the answer is in the question: 10 ÷ 4 =104 = 52 = 212 .

Ask students to reflect on their investigations related to sharing food.

What makes a method of sharing efficient? Explain your thinking. When might this not be the case? What number would you need to share by to easily be able to convert to a decimal answer ($10 ÷ 4 or 10 m ÷ 4)?

Extension

How would you share 8 bars between 5 friends or share 10 licorice straps between 3 friends?