Proportional reasoning: Video and teaching guide

Use this video as a springboard to explore scaling or proportional thinking, and to apply that thinking to a food-related context, drawing on reasoning and mathematical modelling.

This video uses the scenario of two friends wanting to cater for a large group of people for an upcoming celebration. The recipes used will make a certain quantity or serving size. By scaling the recipes for mini pizza bases and cake pops, the friends can make the exact number of bases and cake pops needed. This shows that numbers can be either scaled up or scaled down, to suit any serving size.

Australian Curriculum V9 Mathematics
Years 7–8: Number
AC9M7N06, AC9M7N08, AC9M7N09, AC9M7M06, AC9M8M07

Numeracy Progression
Additive strategies: P10
Interpreting fractions: P8
Multiplicative strategies: P9, P10
Proportional thinking: P2, P3, P6
Understanding units of measurement: P8

*P stands for Progression level

Watch the video below with your students (full screen recommended).

Video duration: 4 min 47 sec

Suggestions to follow up video

Objective: To understand how to reason through problems that involve proportions with fractions.

These tasks involve calculations using mixed numbers and ratios to focus students on ways to manipulate fractions. Recipes we use may need to be converted to suit the serving size required. There are various ways of approaching these tasks, so students have an opportunity to explain their thinking. Breaking the task into smaller parts and using addition works, however, the goal is to move students toward multiplicative strategies.

A number of balls of pizza dough.

A number of balls of pizza dough arranged in three rows of 6.

Role of teacher: Make explicit that all ingredients scale. If the recipe serves 4 people, then to create any multiple of 4 serves, for example, 8, 12 or 16, all the ingredients must be multiplied or repeatedly added. The challenge is when the required number of serves is not a multiple of 4. How can we scale 4, if 18 serves are needed? Ask students how they think they can scale 4 to create the remaining two serves needed.

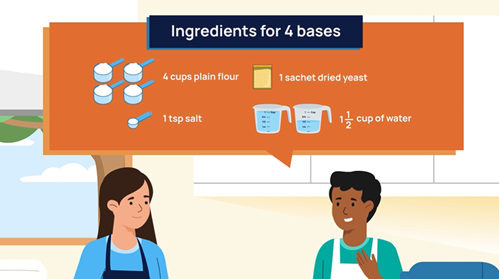
Two people in kitchen aprons.

Two people are wearing aprons in a kitchen. Above the two people is text in a box showing the ingredients to make four pizza bases. A labelled image of each ingredient is shown. Four measuring cups have the text label 4 cups plain flour, a teaspoon is labelled one teaspoon salt, a sachet is labelled 1 sachet dried yeast. Two measuring jugs, one full and the other half full, is labelled one and a half cups of water.

Objective: To use repeated addition to scale up a recipe to the number of serves needed.

Two people in kitchen aprons.

Two people are wearing aprons in a kitchen. Text in a box above them shows how a recipe for 4 serves can be scaled up to 18 serves. The box shows icons for 18 people; 9 grouped in one row (four, four and one) and another 9 people grouped in the same way underneath. Text above says, ‘For 18 people’. Text on screen also includes ‘4 x each ingredient + ½ of each ingredient’.

The recipe for 4 serves can be scaled to 18 serves by realising that 16 is a multiple of 4 (or 4 + 4 + 4 + 4) that is close to 18. The remaining 2 serves can be made by halving all ingredients for 4 serves. Halving for friendly numbers is simple (half of 4 cups is 2 cups; it is not taking away 2 cups of flour) but when the amounts to halve are odd numbers or fractions such as 1 12 or 32 cups of water, how could this be worked out?

One possible strategy is to break up the 1 12 cups into 1 cup and 12 cup to halve ingredients. As there is not one correct method to use, some students may model this as 3 half a cup sizes, which, when halved, would be 3 pieces the size of a quarter cup or 34.

 

Child in a kitchen apron.

Child wearing an apron in a kitchen with ingredients to make pizza dough. Images of measuring cups are used to show how to halve the water ingredient of the recipe. The heading text reads We can break it up, and beneath is shown an equation showing half of one full measured cup of water equals half a cup of water. Then beneath that a second equation shows half a measuring cup half-filled with water equals a quarter of a cup of water.

Objective: To use multiplicative thinking to scale up a recipe to the number of serves needed.

Role of teacher: If students realise that 9 x 2 serves gives 18 serves, then halving the ingredients for 4 serves and then scaling up by a factor of 9 will also create the number of serves required. Is finding half simpler than scaling to one serve and multiplying by 18?

Students may observe that the size of the unit does not change the relationship between numbers. For example, 34 cup or 3 pieces of a quarter cup size, when multiplied by 9 is 9 x 34 or 27 pieces of size a quarter cup, 274 . When using a measuring jug, it may be simpler to measure out 6 full cups and another 34 or 6 34 cups rather than filling the  cup 9 times.

 

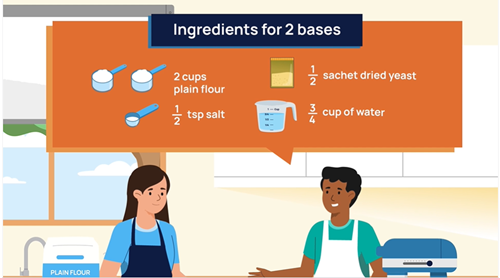
Two people wearing aprons in a kitchen.

Two people are wearing aprons in a kitchen. A text box title says, ‘Ingredients for 2 bases’. Below this text box are ingredients: Two measuring cups are shown with text 2 cups plain flour. A half-filled sachet is labelled ½ sachet dried yeast. A teaspoon is labelled ½ teaspoon salt. A measuring cup containing water is labelled ¾ cup of water.

 

Two people wearing aprons in a kitchen.

Two people are wearing aprons in a kitchen. A text box title says ‘Ingredients for 18 bases’. Below this text, square brackets encase the following ingredients: Two measuring cups are shown with text 2 cups plain flour. A half-filled sachet is labelled ½ sachet dried yeast. A teaspoon is labelled ½ teaspoon salt. A measuring cup containing water is labelled ¾ cup of water. Outside the brackets is the number 9 multiplied by, showing all ingredients are to be multiplied by 9.

Two people wearing aprons in a kitchen.

Two people are wearing aprons in a kitchen. A text box title says Cake pops and shows a picture of three cake pops.

Objective: To use multiplicative thinking to scale down a recipe to the number of serves needed.

A recipe for cake pops that serves 24 must be scaled down as only 18 are needed for dessert. This requires scaling down to a factor of 24 that can then be scaled back up to 18.

Role of teacher: Explore why halves (24 ÷ 2 = 12) and thirds (24 ÷ 3 = 8) are less helpful choices for scaling the recipe. Make explicit that we are looking for a number that can multiply to 18 but is also simple to calculate starting from 24. A quarter of 24 is 6, which can then be scaled up to 18 by multiplying by 3. This is the same as noticing that 18 is 34 of 24. The additive thinking strategy would be to find half and then subtract it from the recipe that serves 24 or find half and also a quarter and then add those two amounts.

 

Two people in aprons in a kitchen.

Two people are wearing aprons in a kitchen. A text box title says ‘Ingredients for 24’. Ingredients for cake pop recipe is shown: 2 cups of cake mix, ½ cup of vanilla icing and 2 cups of white chocolate.

 

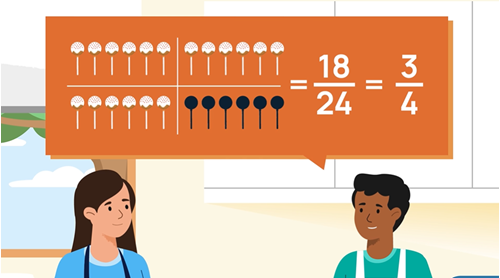
Two people wearing aprons in a kitchen

Two people are wearing aprons in a kitchen. A box shows 24 cake pops arranged as 4 groups of 6. One of the groups of 6 is blacked out to highlight the 18 remaining. The fraction 18/24 = ¾ is shown.

 

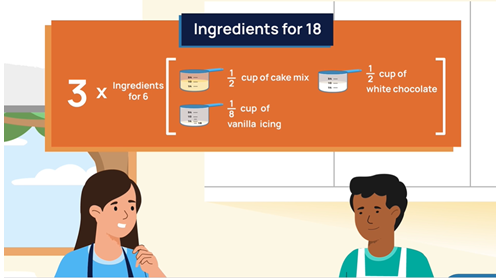
Two people wearing aprons in a kitchen.

Two people are wearing aprons in a kitchen. A text box title says, ‘Ingredients for 18’. Below this text, square brackets encase the following ingredients: A measuring cup labelled ½ cup of cake mix; a measuring cup labelled 1/8 cup of vanilla icing; and a measuring cup labelled ½ cup of white chocolate Outside the square brackets is the number 3 multiplied by ingredients for 6, showing that 3 lots of ingredients to make 6 cake pops will result in 18 cake pops.

Objective: To use scaling to adjust any recipe to the required number of serves.

Role of teacher: Any cook has a standard bank of recipes that they use, and then adjusts them either up or down to suit the number of people to be served. Ask students to find a recipe or give them one such as zucchini soup that serves 2 people: 3 zucchinis, 12 an onion, 1 garlic clove, 2 12 cups water, 4 tsp stock powder. Then ask students to scale up their recipe to feed the class or school population, staff included!

Ask students to reflect on their investigations related to adjusting a recipe to suit the number of people to serve.

Reinforce that there is not one correct method to scale a quantity, but some methods are more efficient than others depending on the information required. For example: whether additive or multiplicative thinking is more efficient for a $60 shirt on sale at 20% off. If you want to know the discount, additive thinking is more efficient (find 20% ( 15 ) of 60) however if you want to know the sale price, $60 – discount, it is more efficient to find 80% of $60 as it gives the value in one step (multiply) not two (multiply to find 20% then subtract). These ideas are also important when dealing with financial calculations such as loan repayments where there are two components, interest and payment made to reduce principal, using multiplicative not additive thinking.