Algebraic equations: Video and teaching guide

Use this video as a springboard to explore algebraic thinking, and to apply that thinking to a financial context, drawing on reasoning and mathematical modelling.

The video uses the scenario of three young people sharing a taxi ride, each travelling a different distance, and working out a fair way to share the cost. The friends need to decide on a departure time based on taxi fares that change rates after 11:00 pm. We show how to develop algebraic equations to calculate the taxi fare and generate tables of values which are plotted on a Cartesian plane to observe the relationship.

Australian Curriculum V9 Mathematics
Year 7–8: Algebra
AC9M7A04, AC9M7A05, AC9M7A06, AC9M7N09, AC9M8A03

Numeracy Progression
Multiplicative strategies: P7
Understanding money: P7
Number patterns and algebraic thinking: P7, P8

*P stands for Progression level

Watch the video below with your students (full screen recommended).

Video duration: 4 min 37 sec

Suggestions to follow up video

Objective: To understand that taxi fares have two components: flag fall and rate per kilometre, and make connections between cost of trip and distance travelled.

In the video, three friends are in a dilemma about when to depart, as the different taxi fare fee structure impacts the overall cost. The two components of a taxi fare are explained. Two different rates are shown that differ depending on time of departure. Travelling after 11:00 pm incurs a more expensive rate but a cheaper flag fall.

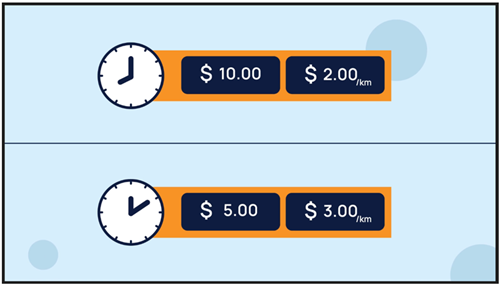
A diagram of a taxi flagfall and rates.

A diagram of a taxi flagfall and rates. Two taxi rates are shown. A clockface shows 8 o’clock with a box divided into two parts. The first part shows 10 dollars, the second part shows 2 dollars per kilometre. A second clockface shows 10 minutes past twelve o’clock with a box divided into two parts. The first part shows 5 dollars, the second part shows 3 dollars per kilometre.

Role of teacher: Make explicit that there are two components to the taxi fee structure: the flag fall cost and the cost based on the number of kilometres travelled. Ask which of these two values is constant (fixed) and which is variable? The constant is the flag fall (no matter how far you travel you will always pay $10.00/$5.00) and the variable is the number of kilometres travelled – the more kilometres travelled the higher the cost of the trip. Ask which fare they would choose and why.

Objective: To represent the relationship between two variables (cost and distance). Create algebraic equations from word problems involving one or more operations.

To assist in solving the problem and determine the cost of each fare, three different methods are presented to demonstrate the relationship between two variables: the cost and the distance travelled.

A table of values

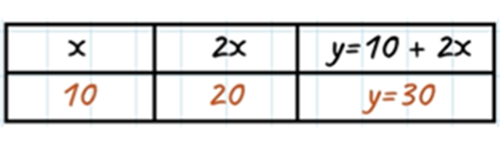
A table of maths with numbers and pronumerals.

A table of maths with numbers and pronumerals. The table shows the values for the equation y = 10 + 2x. The first column shows the value of x as 10. The second column shows the value of 2x as 20. The third column shows equation y =10 + 2x and that y = 30.

An equation

Two equations are noted and text beneath says Compare the equation on a graph.

Two equations are written for comparison: the first equation is 10 + 2x = y. The second equation is 5 + 3x = y. Text under the equations says, ‘Compare the equation on a graph’.

A graph

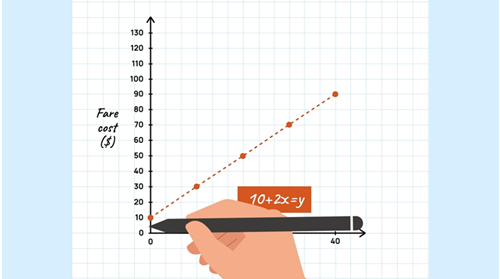
A hand holding a pen and plotted points on a line graph.

A hand holding a pen and plotted points on a line graph. Plotted points are connected creating a line graph. The line graph is labelled 10 + 2x = y. The Y-axis is labelled Fare cost ($) with intervals of 10 from 0 to 130.

 

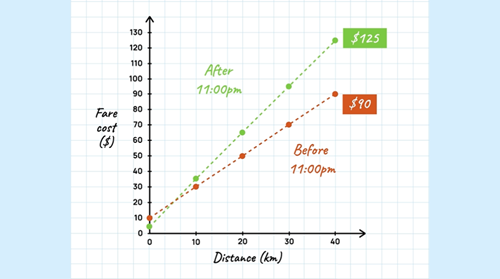
Two line graphs

Two plotted lines are shown on a graph, one green and one brown. The X-axis is labelled ‘Distance (km)’ with intervals of 10 from 0 to 40. The Y-axis is labelled ‘Fare cost ($)’ with intervals of 10 from 0 to 130. Plotted points are connected creating each line graph. The line graph in brown is of the equation 10 + 2x = y. It is labelled ‘Before 11:00 pm’ and another label says $90. The line graph in green is of the equation 5 + 3x = y. It is labelled ‘After 11.00 pm’ and a second label says $125.

Role of the teacher: make explicit that the power of algebra is its ability to generalise the total fare cost (y) for any flag fall value and distance travelled (x). Work through how to write each fare algebraically y=5+3x and the other is y=10+2x. Explain that y is the cost, x is distance travelled.

Summarise and identify costs at the intervals for distance. For example, for a trip of 40km (x = 40) the total cost of each trip would be: before 11:00 pm: 10 + (2 × 40); after 11:00 pm: 5 + (3 × 40).

Present the values in a table to use the functional reasoning.

Table for y = 10 + 2x.

x y
0 10
10 30
20 50
30 70
40 90

Objective: To represent the relationship between two variables (cost) and (distance). Create algebraic equations from word problems involving one or more operations.

In the video, the problem of how to share the ride’s cost fairly is introduced. Each passenger travels a different distance. Ask the students to think about different ways the fare could be shared:

  • each person pays a third
  • each person pays a portion depending on their fraction of the total ride taken.

The proportional distance each person travels.

A map of a town showing three people and a line joining them along the route.

A map of a town showing three people and a line representing a taxi journey past their homes. First up, a child is at a point at one-third of the total journey represented on the line. Secondly, a child is at a point at two-thirds of the total journey represented on the line. Then, lastly, another child is at a point at end of the journey represented on the line.

The fair split equally.

Three people seated in the back of a taxi

Three people seated in the back of a taxi. Above the three people is a table. The top row of the table says $90. The bottom row of the table is divided into three, each containing $30. The table is showing a way to share the $90 taxi fare.

Another way to split the fare is based on the portion each person travels.

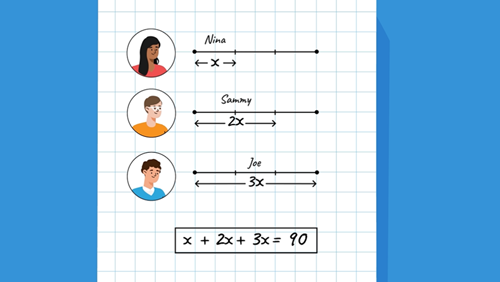
Three people alongside a number line and pronumerals.

Three people, each with a number lines and pronumerals, and a single final equation below. The first person has a number line with x showing one-third of the number line and a label Nina. The second person has number line with 2x showing two-thirds of the number line and a label Sammy. The third person has number line with 3x showing three-thirds of the number line and a label Joe. The equation displayed under the people says x + 2x + 3x = 90.

Role of teacher: make explicit that the steps to create the equation:

x + 2x + 3x = 90

The video also includes another way to write the equation as an option for investigation:

13 x + 23 x + x = 90.

Ask students to reflect on their investigations related to taxi fares.

What makes the biggest difference to cost: a fixed cost or a cost that changes depending on a variable? Explain your thinking. When might this not always be the case?

A new taxi driver comes to town and charges $2.00 flag fall and $5.00 per km. What would it cost to travel 3km and 30km?

Is this fee structure good for short trips or long trips? Explain your answer.