Algebra basics: Video and teaching guide

Use this video as a springboard to introduce algebraic thinking, and to apply that thinking to a financial context, drawing on reasoning.

This video uses the scenario of friends and family saving money to support various charities. By changing the time available to save, the total amount to save and whether or not money has already been saved to be put towards the total, the friends work out how long or how much they need to save to reach their goals. We show how to develop and solve algebraic equations with pronumerals representing the unknown quantity.

Australian Curriculum V9 Mathematics
Years 6–7: Algebra
AC9M6A02, AC9M7A01, AC9M7A02, AC9M7A03

Numeracy Progression
Number patterns and algebraic thinking: P5, P6, P7
Understanding money: P7

*P stands for Progression level

Watch the video below with your students (full screen recommended).

Video duration: 3 min 57 sec

Suggestions to follow up video

Objective: To understand how to use pronumerals to develop an algebraic linear equation to represent raising money and solve for an unknown.

In the video the friends want to raise money to support a charity. Their problem is knowing how long it will take to save the money. The unknown is defined and an algebraic equation is developed. Solving the equation for the unknown allows the friends to know how long it will take to reach their saving goal.

Child in a park pointing to maths equations.

Child in a park pointing to maths equations. The equations shown are y = 4x and 2x + 1 = 20. No value for x is given.

Role of teacher: Make explicit that a pronumeral is defined to represent an unknown number – it doesn’t matter which letter is used. For example, we could say that T = 4 × p where T is the total number of kilometres walked and p is the number of kilometres walked per day. The value of the total (T) varies depending on the value of p, or if I know the total needed, the number of kilometres to walk each day could be worked out.

Objective: To solve one-variable linear equations with counting numbers and verify the solution by substitution.

In this video a problem is presented about raising money for wildlife by getting sponsored for walking a total of 28 kilometres. The unknown quantity (How many kilometres they need to walk each day) is represented by a pronumeral ‘n’. The walk is completed over four days. Algebraically that can be written as 4n = 28.

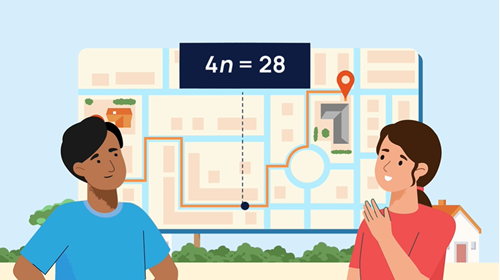
Child and child with a map.

Child and child with a map showing a walking route through town. A box has the equation 4n = 28.

Ask students what is their estimate for 'n' that is definitely more than (lower bound) and definitely less than (upper bound). This will give them an idea if their calculated answer is reasonable. Without working anything out, students should realise that 'n' has to be more than 5 (which would be 4 x 5 = 20) and less than 10 (which would be 4 x 10 = 40).

The next problem involves donating money for injured wildlife. The unknown quantity (How many weeks is needed to save $48) is represented by a pronumeral ‘n’. The person saves $3 a week. Algebraically that can be written as 3n = 48.

A picture of an injured kangaroo, shown on a computer tablet as part of a fundraising request.

A picture of an injured kangaroo shown on a computer tablet, with a call to donate money. Text says Injured kangaroo joey. Donating $48 helps us save this joey. Donate now.

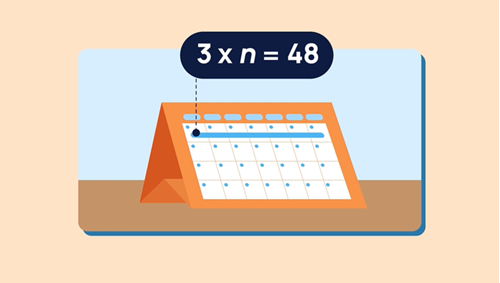
A picture of a calendar with an equation.

A picture of the month of a calendar, with an equation written above. One week of the month is highlighted. The equation shown is 3 x n = 48, and points to day one of the highlighted week.

Ask students how they would solve the equation.

The challenge for students may be that the answer is larger than their known times tables (> 10). Students who are count all/additive thinkers may draw three circles and put dots in each circle until they have shared the 48.

Objective: To formulate algebraic equations using constants (amount already saved), variables (number of weeks to save and amount to save each week) and operations. Create algebraic equations from word problems involving one or more operations.

In this problem Lucy has already saved $9. The unknown quantity (How many weeks is needed to save $48) is represented by a pronumeral ‘n’. We know Lucy saves $3 a week. Algebraically that can be written as 9 + 3n = 48.

A child with money.

A child with money and a jar to save money in. A text box says, ‘If Lucy has already saved $9’.

 

Role of the teacher: the power of algebra is its ability to generalise for any variable (number of weeks, amount saved per week) and include an amount that has already been saved. If money has already been raised, do students expect this to reduce or increase the number of weeks needed to save the total amount of money?

How would students work out the unknown number of weeks, n, of saving needed?

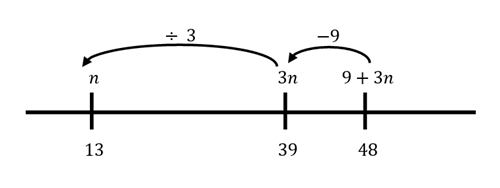
An alternative method for students to solve this equation is to think of a number line. Wherever you place 3n, 9 + 3n will be to the right (greater than). This is equal to 48.

So 3n will be 9 less than 48.

The final step is to divide by 3.

A number line showing an algebraic equation.

A number line is used to represent the equation 9 + 3n. On the left-hand side of the number line, n is marked as equal to 13. 3n is shown along the number line to the right equal to 39. Next along the number line to the right, adding 9 to 3n is shown equal to 48. If we read from right to left from 9 + 3n, if we subtract 9 we have 3n. And then moving further along to the left, if we divide 3n by 3 we get back to n.

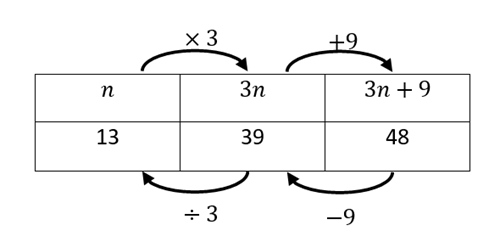
Alternatively, the equation can be built as follows (each set of vertical boxes are equal, for example, 3n + 9 = 48). The top row is built starting with , moving right until the equation is complete. Then the processes are reversed to determine the value of n.

A table showing pronumerals and numbers.

A table showing pronumerals and numbers to represent the equation 9 + 3n. On the left-hand side of the number, n is marked equal to 13. 3n is shown along the number line to the right equal to 39. Next further along adding 9 to 3n is shown equal to 48. If we read from right to left from 9 + 3n, if we subtract 9 we have 3n. And moving again to the left, if we divide 3n by 3 we get back to n.

Ask students if it is possible to ÷ 3 first instead of −9? Prove that the result would be the same.

  • Yes, it is. However, many students are often confused by the fractions produced (the numbers in this example are friendly and don’t result in fractions) or forget to divide all parts of the equation. In this case, the result would be 3 + n = 16, n = 13.

Ask students to reflect on their investigations related to solving equations.

Reinforce that there are actually four parts (y, x, c, m), so you must know at least 3 to be able to solve the equation.

This is an introduction to a linear function: y = mx + c or y = a + bx

            The total amount to be saved (y).

            The amount saved per time period (m or b).

            The number of time periods that you will save for (x).

            The amount of money already saved (c or a).

Students can design their own savings scenario and have other students solve it.

A child and an equation.
A child and an equation, 9 + 3n = 48.
 A child and two equations.
A child and two equations, 12 + 4n = 48, 12 + 4n = 100.