Area and perimeter: Video and teaching guide

Use this video to explore concepts of area and perimeter, and connect these ideas to real-world situations.

The video introduces area and perimeter of rectangles using practical scenarios of tiling, laying carpet, building a garden bed, and the use of safe distancing in public spaces.

The video includes clear definitions and visual representations of area and perimeter. The lesson invites viewers to use reasoning when exploring, understanding and making calculations.

Australian Curriculum V9 Mathematics
Years 4–6: Measurement
AC9M4M02, AC9M5M02, AC9M6M02

Numeracy Progression
Understanding units of measurement: P6, P7, P8

*P stands for Progression level

Watch the video below with your students (full screen recommended).

Video duration: 3 min 15 sec

Suggestions to follow up video

Objective: To understand what area and perimeter mean, and clearly differentiate them from each other.

In the video, area is defined as ‘the space taken up by a flat shape and is measured in square units’.

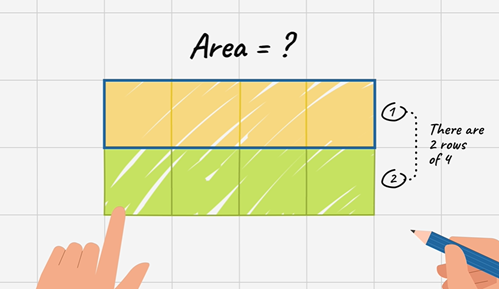
Students hands, pencil in one hand, working with drawn rectangular shape defining area.

Students hands, pencil in one hand, working with a drawn rectangular shape showing area. This rectangle is divided into 8 squares made up of two rows each containing 4 squares. Text says, ‘There are 2 rows of 4’. Above the rectangle is the question, Area equals question mark. No solution is shown.

In the video, perimeter is defined as ‘the total length of the shape’s outer boundary’.

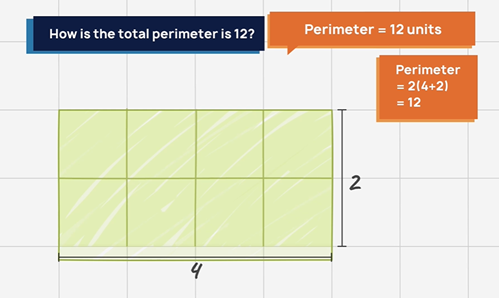
Rectangular shape showing perimeter.

Rectangular shape showing perimeter. The rectangle is divided into 8 squares made up of two rows each containing 4 squares. Text above the rectangle says ‘How is the total perimeter 12?’ Text in a caption says ‘Perimeter equals 12 units’. A box to the side of the rectangle shows the perimeter calculation, Perimeter equals 2(4 +2), which equals 12.

Role of teacher: Ensure students clearly understand that:

  • area is the space enclosed by the boundary of a shape
  • perimeter is the total length of the outer boundary of that enclosed space.

Objective: To understand and use methods for working out the area of a rectangle.

In the video (01.03), students are invited to think about and work out the total area of a 2D shape.

Pause at this point for students to think about:

  • What is the area of this shape in square units?
  • What strategy did you use to calculate the area?

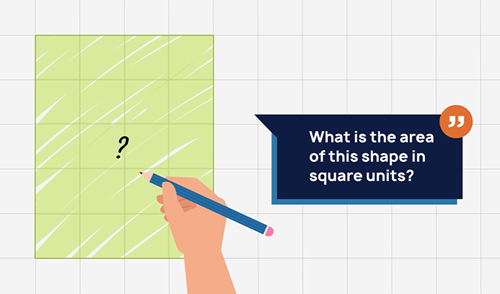
Rectangular shape showing shaded grid squares and a question mark prompt and to the right the question text, ‘What is the area of this shape in square units?’

Rectangular shape showing shaded grid squares and a question mark prompt and to the right the question text, ‘What is the area of this shape in square units?’. The rectangle is made up of five rows each containing 4 squares. No answer is given.

Student strategies may include:

  • seeing a length of 5 units and a width of 4 units and knowing that L x W (5 x 4) gives an area of 20 units
  • seeing two vertical rectangles of 10 squares, and doubling that
  • skip-counting rows of four 5 times (4, 8, 12, 16, 20)
  • skip-counting rows of five 4 times (5, 10, 15, 20).

Role of teacher: 

  • Help students understand and make connections between different strategies for calculating area.
  • Invite students to think about which strategies for calculating area make sense to them and why.

Objective: To apply knowledge and use reasoning to explore a problem about area.

Provide students with 1cm square grid paper. Pause at the point in the video (01.23) where the shapes have 24 square units. Give students time to:

  • Look at the two rectangles. What do you notice? What do you wonder?
  • What other rectangles have an area of 24 square units? How will you know when you’ve found them all?

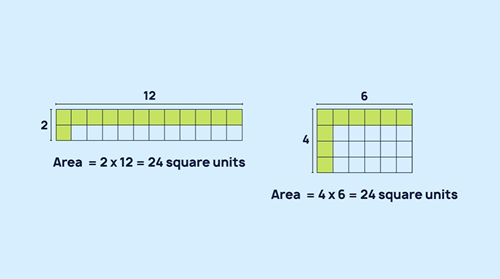
Two different rectangular shapes with gridded squares, each with the same area.

Two different rectangular shapes of gridded squares, but each with the same area. One rectangle is made up of two rows each containing 12 squares. Text below it says Area equals 2 x 12, which equals 24 square units. The second rectangle is made up of four rows each containing 6 squares. Text below it says Area equals = 4 x 6, which equals 24 square units.

Role of teacher: 

  • Provide students with access to grid paper and sufficient time to find all possible rectangles with an area of 24 square units.
  • Encourage the use of strategies for calculating area that are more efficient than counting squares, for example, knowing that 2 rows of 12 can be written and calculated as 2 x 12 = 24.
  • Actively invite students to think of ways that they can prove they’ve found all possibilities.

Objective: To develop a deeper understanding of area and perimeter by exploring if there is any relationship between the two.

Provide students with grid paper and a pencil.

Pause at this point in the video (01.51). Invite students to look at this table and think about:

  • What do you notice? What do you wonder?
  • Why is this table interesting? Why is it useful?

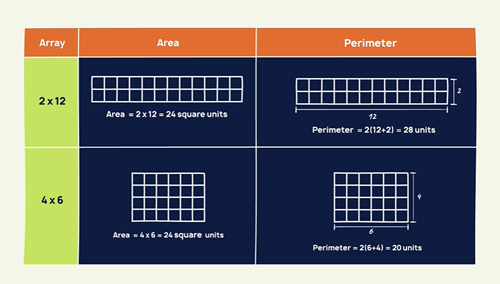
Two different gridded rectangular shapes each with the same area and showing different perimeters.

Table with three columns with the headings from left to right: Array, Area and Perimeter. The table has two rows of information. In the first row the first column has 2 x 12 for the ‘Array’. The next column for ‘Area’ shows a rectangle made up of two rows, each containing 12 squares. Text below says Area equals 2 x 12, which equals 24 square units. The next column for ‘Perimeter’ has the rectangular shape also made up of two rows, each containing 12 squares with the label 12 along the bottom row and the label 2 alongside the rows. The text below says Perimeter equals 2(12+2), which equals 28 units. In the second row the first column has 4 x 6 for the ‘Array’. The next column for ‘Area’ shows a rectangle made up of four rows, each containing 6 squares. Text below says Area equals 4 x 6, which equals 24 square units. The next column for ‘Perimeter’ has the rectangular shape also made up of four rows, each containing 6 squares with the label 6 along the bottom row and the label 4 alongside the rows. The text below says Perimeter equals 2(6+4), which equals 20 units. The table shows that area and perimeter can be different.

In the video, the following question is posed:

  • Is it possible for two shapes to have the same perimeter but different areas?

Objective: To connect prior knowledge and ideas to formal notation used to calculate area and perimeter.

Rectangular shape of gridded squares with a hand holding a pencil.

Rectangular shape of gridded squares with a hand holding a pencil. The rectangular shape is 4 rows of squares across and 5 rows of squares down.

Use the video to support explicit teaching of formulas used to calculate area and perimeter.

Formula for calculating area:

  • L x W

Formulas for calculating perimeter:

  • L + L + W + W
  • (2 x L) + (2 x W)
  • 2L + 2W

Role of teacher:

  • Facilitate whole-class discussion for students to share their findings and reasoning. Where beneficial, record student ideas involving arithmetic and visual representations on the board.
  • Help students recognise that there are different ways to work out area and perimeter. Encourage them to think about why different ways make sense, and which methods they personally prefer.