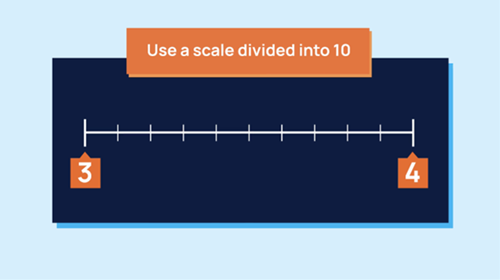
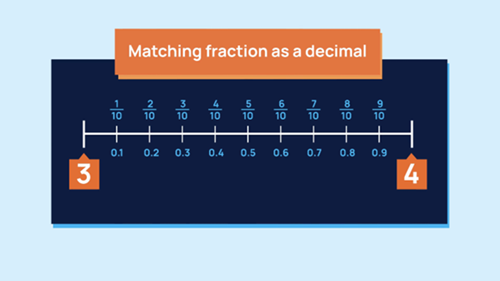
Representing one divided into 10 equal parts
Objective: To develop the language of tenths to describe one whole divided into ten equal parts.
In the video, the situation of measuring the mass of apples on a kitchen scale is used to introduce the need for more accurate measurements than using whole numbers.
A number line is used to show how one whole can be divided into 10 equal parts. This can be used to introduce tenths.
Role of teacher: Ensure students clearly understand:
- why we need decimal fractions as a more accurate measure
- that when dividing a whole into 10 parts we use tenths
- the connection between the decimal fraction and the decimal notation.
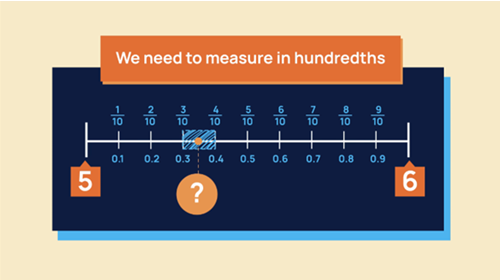
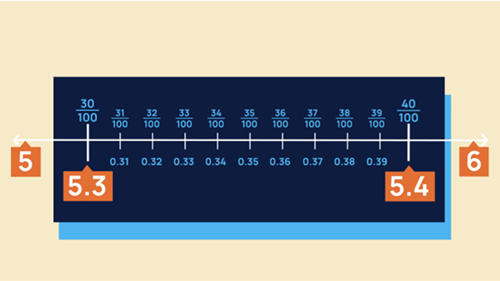
Representing one divided into 100 equal parts
Objective: To develop the language of hundredths to describe one whole divided into 100 equal parts.
In the video, the situation of measuring an athlete’s long jump is used to introduce the need for a more accurate measurement than using tenths.
A number line is used to show how one-tenth can be further divided into 10 equal parts. This can be used to introduce hundredths.
Role of teacher: Ensure students clearly understand:
- why we need decimal fractions as a more accurate measure
- that when dividing a whole into 100 parts we use hundredths
- the connection between the decimal fraction and the decimal notation.
Recording and expressing decimal fractions
Objective: To express decimal fractions as mixed numbers, using decimal notation and place value.
In the video, you may notice that we do not name numbers using terminology such as ‘three point six’ or ‘five point three five metres’. Instead, we say three and six-tenths for 3.6 (decimal notation) or five and thirty-five-hundredths for 5.35.
Note: students often experience difficulties with decimal fractions when place value is not used in naming numbers. For example, it is advised that students use place value to name the number, such as, 2.75 is two and seventy-five-hundredths rather than spelled out as separate digits such as ‘two point seven five’.
In the video, the number 5.35 is represented in decimal notation (5.35) as a mixed number five and thirty-five-hundredths and showing the place value parts of ones, tenths and hundredths.
Role of teacher:
- Encourage students to use place value when naming decimal numbers.
- Provide students with the 5.35 example shown in the video, then have them choose their own number to express in different ways.
- Explain that the decimal point separates the whole number part of a number from its decimal part.
Compare and order decimals
Objective: To compare and order decimals using a number line.
In the video, the numbers for a high jump competition are shown as 5.35, 5.04 and 5.9.
Pause the video at this section and ask students to compare and order the decimals largest to smallest. Share results and ways they worked out the order.
In the video, it is said that ‘zero has an important role’:
- Ask students to explain what this means, using examples.
Role of teacher:
- Encourage students to use place value when naming decimal numbers.
- Use the numbers 5.35, 5.04 and 5.9 from the video as a worked example to run a number talk about ordering decimals.
- Provide other numbers for students to order smallest to largest and largest to smallest.
- Provide two decimal numbers and ask students to identify two numbers that fit within that range. Show using a number line.