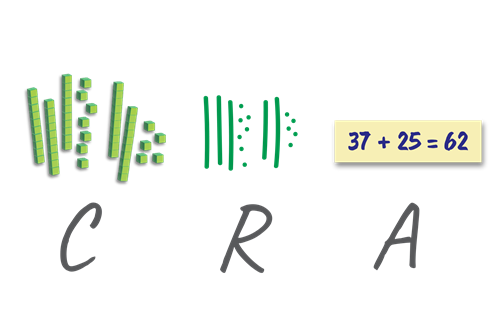Concrete, Representational, Abstract (CRA)
Overview
The Concrete, Representational (Pictorial), Abstract (CRA) model is based on Jerome Brunner’s theory of cognitive development: enactive (action-based), iconic (image-based) and symbolic (language-based). Typically, a child will start by experiencing a new concept in a concrete, action-based form. They move to making a representation of the idea, in pictures or more sophisticated diagrams, and then to using abstract, symbolic notation. Students do not always pass through these stages in a linear fashion, nor are they specific to particular age groups. Students are able to build visual models of complex ideas that help to deepen their learning.
Although concrete manipulatives are common in lower primary years they can (and should) be used throughout schooling. There are many virtual manipulatives (digital representations of concrete manipulatives, not games) that can be used when the physical manipulatives are not available.
When using manipulatives, it is important that the connections to the mathematics being learnt are made clear, as well as providing clear instructions on how to use the manipulative.
The teacher:
- explains the learning intention for the lesson
- models the concept using a manipulative
- explains how to use the manipulative in connection to the specific concept being taught
- allows students time to familiarise themselves with the concrete (virtual) materials
- demonstrates how to annotate and represent the physical objects, moving students to the representational stage
- connects the abstract notation to the concrete and representational stages
- plans lessons with the use of concrete or virtual materials embedded
- ensures concrete or virtual manipulatives are available in the classroom
- creates a classroom culture where using concrete materials is common for all learners.
The students:
- know how to use a range of concrete or virtual manipulatives
- feel comfortable to use concrete or virtual manipulatives in their learning
- can make the connections between the concrete materials, drawings and abstract notation
- know when they have achieved the lesson goal – feel success.
Watch this video, which describes ways to use a range of strategies including different representations to help students make meaning in their maths lessons.
Examples of the strategy in action

Manipulatives in the primary classroom
Guidance on how to use manipulatives in primary year levels.
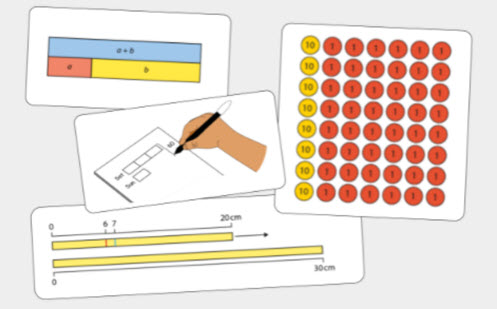
Using mathematical representations
Guidance on how to use manipulatives in secondary year levels.