Developing flowcharts: Halving strategy
Year level: 4
Strand: Number / Algebra
Lesson length: 60 mins
In this lesson, students will create a flowchart outlining the sequence of steps required when using the halving strategy for division. The process of creating the flowchart consolidates the sequential steps required when solving problems and can be found in other learning areas, such as Design and Technologies and Digital Technologies.
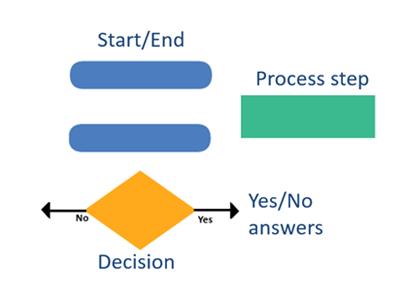
Curriculum information
Achievement standard
Students follow and create algorithms that generate sets of numbers and identify emerging patterns.
They use mathematical modelling to solve financial and other practical problems, formulating the problem using number sentences, solving the problem choosing efficient strategies and interpreting results in terms of the situation.
They use their proficiency with addition and multiplication facts to add and subtract, multiply and divide numbers efficiently.
Content descriptions
Students learn to follow and create algorithms involving a sequence of steps and decisions that use addition or multiplication to generate sets of numbers; identify and describe any emerging patterns. AC9M4N09
Students learn to develop efficient strategies and use appropriate digital tools for solving problems involving addition and subtraction, and multiplication and division where there is no remainder. AC9M4N06
Students learn to recall and demonstrate proficiency with multiplication facts up to 10 x 10 and related division facts; extend and apply facts to develop efficient mental strategies for computation with larger numbers without a calculator. AC9M4A02
Students follow and describe algorithms involving sequencing, comparison operators (branching) and iteration. AC9TDI4P02
General capabilities
Numeracy
Digital Literacy
- select and operate tools
Critical and Creative Thinking
- Analysing
- Inquiring
Assessment
- Peer assessment – have students follow their partner's flowchart to check for purposeful sequence of steps. Provide feedback to peers.
- Students can find evidence in their work that meets the success criteria after feedback has been given. Ask students to evaluate their level of success based on their success criteria reflection. This can be in the form of a Kahoot, an exit slip or class discussion.
Prerequisite student knowledge and language
- understands that halving is splitting (dividing) a number into 2 equal groups
- represents the division of numbers using the halving strategy, for example, 10 divided by 2 = halve 10 = 5
- applies mental strategies for halving to division of 4, for example, to divide 96 by 4, halves 96 then halves 48 to get 24
Areas of challenge
Some students:
- may need further scaffolding with number fact knowledge for multiplicative thinking and division
- may have difficulty visualising the flow of the steps without performing the task
- may include additional ‘branches’ that hold no purpose to the outcome
- may focus on a particular part of the flowchart and ignore the other aspects
- find it difficult to decide what information is necessary and useful to perform the task
- may not recognise or make the connection between halving and dividing by two.
What you need:
Lesson plan (Word)
Teacher’s slides (PowerPoint)
Digital software programs that provide information on flowcharts: Digital Technologies Hub
Digital software programs to build flowcharts such as Miro, Lucidchart, Creately and Smartdraw. (Decisions about what software to use should be based on your school’s policies.)
Learning goals
Learning intention
- We use flowcharts to provide a visualisation of the steps required to perform mathematical procedures.
- We can use a flowchart to model the halving strategy so that we can show the steps involved in solving simple division problems.
- We create ways to test the steps of the strategy when solving simple division problems.
- We can provide and accept feedback to refine the steps in a flowchart.
Success criteria
By the end of this lesson, students can:
- describe the steps when using the halving strategy
- create a flowchart representing (or modelling a series of) steps, using graphics
- follow an algorithm to show the steps involved in solving division problems
- test the validity/accuracy of a flowchart and provide constructive feedback.
Why are we learning about this?
Teacher perspective:
When developing flowcharts (or algorithms) using branching, students are thinking critically about the precise steps required to achieve an outcome (or to find a given number). By learning how to use branching, students develop skills in logical thinking and decision-making. They can understand how to design algorithms to perform different actions to enable more complex problem-solving. The ability to design algorithms with branching is a transferable skill that can be utilised in other learning areas (for example, Design and Technologies and Digital Technologies).
Learning hook 15 mins
Download and use the teacher’s slides to accompany your teaching. You will find this in the ‘What you need’ section.
Why are we learning this? This question asks students to think about using visual steps to solve division problems. (slide 2)
Pose the following questions to the class: (slide 3)
- What is the same?
- What is different?

Slide 3
On slide 4 and ask the following question referring to a new set of arrays. ‘What is the same and what is different about these images?’
Use slide 5 to explain to the class that all images show 12 split into 2 equal groups – some horizontally and some vertically. The collections have been halved to represent the connection between halving and dividing by 2, as well as the visual concept of symmetry.
Explain that we can represent the connection between all images using number sentences. These sentences represent how we can use the halving strategy when dividing numbers by 2. For example, all of these sentences below are ‘equivalent’.
12 halved
half of 12
12 ÷ 2 = 6
The hook
Use slide 6 to explain to the class that concepts about division and halving can be represented using a simple flowchart. To create a flowchart, we need to visualise the anticipated outcomes, sort these and then present choices that can be made. To create a flowchart for dividing by 2 (halving), we need to reflect on the series of steps taken to solve division problems.
Flowchart task
Ensure you have prepared a bag of 12 counters and hold them in your hands but don’t tell the class that there are 12.
Perform a ‘think aloud’ for developing a flowchart for dividing by 2 (halving) by modelling the steps required to halve a collection (share between 2).
Use questioning as you model the steps, ‘Can I divide the bag of counters equally between 2, or in other words, is the solution a whole number?’
Present the counters and ask the class, ‘How can we split these counters to model dividing by 2 (halving)?’
Model the task by dividing the group of counters into 2 equal groups recording the series of steps on the board.
For example, you might say:
‘When dividing by 2:
- Can the whole number be divided equally between 2? Yes.
- Do the groups form 2 whole numbers?
- Yes: How many will each group receive? X (solution)
- But what if the answer is no? What does this mean? You cannot divide this number by 2 to achieve a whole number solution. Students may also make links to odd and even numbers.
Show slide 7 and ask the class: how could we present this in a way so that it is easy to ‘see’.
Show the following flowchart to the class using slide 8.
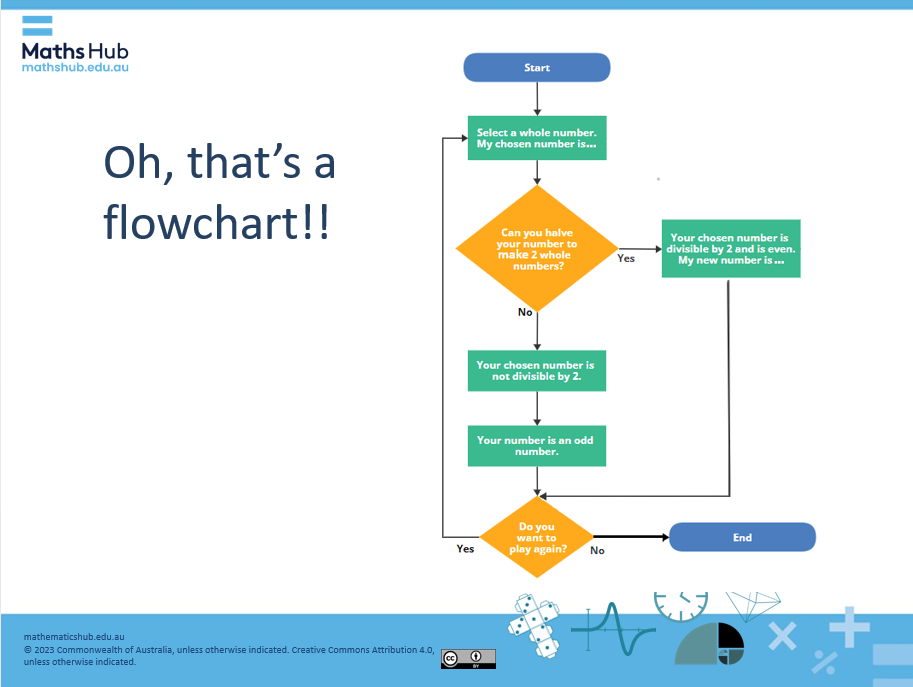
Slide 8
Explain and show the properties of a flowchart and ask or talk about why flowcharts work so well, such as:
- that the steps are presented in a logical order to create a path/sequence to follow
- you can build a flowchart for just about any purpose
- that with a few simple shapes and arrows (branches), you can visualise an idea or action required to achieve an outcome
- that a flowchart allows ideas to be presented in a meaningful way
- that the visual display breaks down the steps so the process is easier to understand, follow and check
- that there is minimal text and creative design used to provide directions.
Explore 30 mins
Questioning
Using slide 9 instruct students that they are going to create their own flowcharts, either in their workbooks or on some butcher’s paper. Before they begin, reflect on the thinking involved to divide a number by 2 using halving. As a group, ask questions to stimulate creative thinking.
- How could we use this information to help us divide numbers by 4? For example, if we can use doubles to multiply by 4 (double, double), could we use halving to divide by 4? (To calculate 4 x 15 we can double 15 = 30 and then double 30 = 60. What if we were to find 60 ÷ 4? How could we use the halving strategy to support us with this process?
- What connections are there between dividing by 4 and the halving strategy?
- What about dividing numbers by 8? What connections can we make between doubling and halving to support this process? For example, if we can use doubles to multiply by 8 (double, double, double) could we use halving to divide by 8?
- What actions/steps do you take in your thinking to complete this sequence?
- Ask students to think about the sequence of steps required for the intended outcome. How can you present these steps in the form of a flowchart?
Task: students can work in pairs, small groups or individually
Ask students to create a flowchart that describes the sequence of steps required to divide numbers by 4. Ensure you encourage students to be creative with the shape and branch designs. Let them know that everyone thinks differently and that different ideas can still lead to the correct answer.
While students are working, ask students to think about the following reflecting question: ‘If numbers are not divisible by 2, 4 (or 8) and have remainders, are they always odd numbers?’
Once students have created their flowchart, arrange for students to share their chart with a peer to test and provide feedback. Instruct the peers or assessors to give feedback on the sequence and whether the intended outcome was achieved.
Once students have reviewed a peer’s flowchart, pair them up (or in small groups or as a class) and use ‘questioning’ to help draw out the main concepts in the topic: number sequences, remainders, division.
- What patterns can you ‘see’ between the number equations involving dividing by 2, 4 and 8?
- What connections can you make between dividing by 2, 4 and 8 and the halving strategy?
- What do you notice about the numbers that can be divided equally by 2, 4 and 8 and the ones that can’t (result in remainders)?
- What statements can you make about the halving strategy?
Explain the symbols and instruct students to begin their own flowchart (slide 10).
Guide students with more questioning, ‘What is a condition you use to decide if you can divide a number by 2? Record this condition inside the first shape. What could the possible responses be? This will help you decide how many branches you will need initially.’
Differentiation (enabling): Provide an empty flowchart template. Include start, true and false.
Differentiation (extending):
- Use slide 11 to extend sudent, ask ‘how could we create a flowchart that combines dividing numbers by 2, 4 and 8 and the connection with the halving strategy?’
- ‘What conjectures can you make about dividing by 2, 4 and 8 and the halving strategy? Is your conjecture always true? How do you know?’
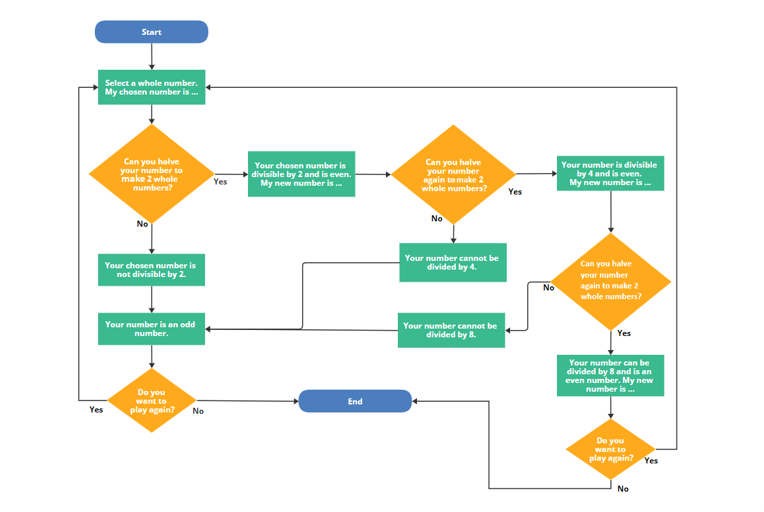
Slide 11
Summary and reflection 15 mins
Use the following questions to summarise the learning intentions and reflect on the success criteria (slide 12).
- What connections do you make between dividing by 2, 4 and 8 and the halving strategy? How could we use this information to help us solve division problems with larger numbers? For example, 240 divided by 4.
- Why is it important to visualise (or record) the steps when developing a flowchart?
- What are some of the strategies you used to create your flowchart today?
- What impact did the feedback from your peer have on the outcome of your flowchart?