Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M5N06, AC9M5N07
Numeracy Progression: Interpreting fractions: P8, Multiplicative strategies: P7
At this level, students learn efficient ways to multiply and divide numbers using increasingly sophisticated strategies. They develop flexible strategies to solve multiplication facts and related division facts and consolidate automatic recall. They identify and describe factors and multiples of whole numbers and use them to solve problems.
Use classroom talks to help students work collaboratively to build their strategies to solve multiplication problems.
- Show how a doubling strategy can simplify a multiplication problem.
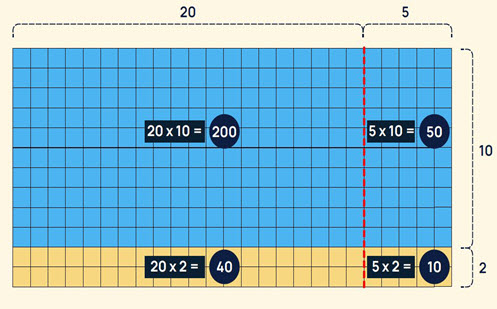
- Model place value partitioning strategies to multiply larger numbers by one-digit and two-digit numbers. For example, to multiply 24 x 12, first multiply 10 x 24 and then multiply 2 x 24 and add the two products together. Use area models and arrays to show partitioning.
- Make explicit how factors can be used to simplify calculations. For example, 15 x 16 can be simplified into 5 x 3 x 4 x 4 and rearranged to 5 x 4 x 3 x 4 = 240 to make the calculation easier. The rearranging of these numbers contextualises the commutative and distributive properties of multiplication.
Provide opportunities to solve division problems presented as number stories in familiar contexts. Where there is a remainder, have students interpret the meaning and represent the problem. Discuss the situations where a remainder needs to be rounded, for example, when dealing with passenger numbers on a train.
Encourage students to solve simple division problems mentally drawing on the known multiplication facts. For example, when given the problem of sharing 36 stickers between 9 people, students see the problem as 36 divided by 9 and use their times table facts of 9 x 4 = 36 to work out how many 9s make 36.
Teaching and learning summary:
- Develop efficient strategies for multiplying and dividing numbers.
- Connect concrete, visual and abstract representations of multiplicative situations using familiar contexts.
- Interpret and represent the remainder in division calculations.
Students:
- solve problems involving multiplication of large numbers by one-digit or two-digit numbers using efficient mental strategies, written strategies and appropriate digital technologies
- solve problems involving division by a one-digit number, including those that result in a remainder
- identify and describe factors and multiples of whole numbers and use them to solve problems.
Some students may:
- say ‘3 into 15’ to solve the division problem, which may indicate they have limited understanding of the meaning of division
- have little understanding of what the remainder represents
- have difficulty matching materials and representations to number problems
- get confused when a division answer includes a zero, for example, when dividing 6,540 by 5, they don’t record 0 as it means nothing so write the answer as 138 instead of 1,308.
To address these problems, use classroom talks to show different representations of division, using correct terminology when discussing division problems, and using efficient strategies to solve the problems. Discuss problems with and without remainders and use examples to show what the remainder means.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning that division is the ‘sharing’ of items, and that sometimes division can result in remainders if the items can’t be evenly shared.
Why are we learning about this?
- Being able to fluently divide numbers and explain my thinking builds number sense and is helpful when solving more complex problems.
What to do
- Open the link to the Remainders game.
- Watch the video to learn how to play the game.
- Collect the resources listed below the video. Note: if you don’t have counters, find 24 objects that are the same items, for example, paperclips or pasta shells.
- Play the game with a friend or family member.
Success criteria
I can:
- solve problems involving division and explain my thinking.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Concrete, Representational, Abstract (CRA model)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Collaborative learning
For group work to be effective students need to be taught explicitly how to work together in different settings, such as pairs or larger groups, and they need to practise these skills.
Go to resource -
Multiple exposures
Providing students with multiple opportunities within different contexts to practise skills and apply concepts allows them to consolidate and deepen their understanding.
Go to resource -
Classroom talks
Classroom talks enable students to develop language, build mathematical thinking skills and create mathematical meaning through collaborative conversations.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
reSolve: Multiplication: reSolve bakery
A series of inquiry-based lessons that investigate strategies for multi-digit multiplication.
Go to resource -

reSolve bakery 1
This video invites students to reason in different ways when calculating the total in an array, encouraging the use of mental multiplication strategies.
Go to resource -

reSolve bakery 2
This video models and compares different multiplication strategies for solving a mathematical problem.
Go to resource -

reSolve bakery 3
This video models and compares different multiplication strategies and draws on various concepts, including two-digit multiplication, shape and area.
Go to resource -

Using mates
In this lesson, students solve problems using the associative rule.
Go to resource -

Growing garlic
Use this interactive tool to discuss remainders in division problems.
Go to resource -
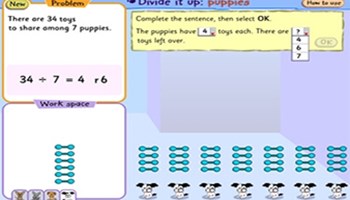
Divide it up: puppies
Use this interactive game to learn about equal sharing and division, including a remainder.
Go to resource -
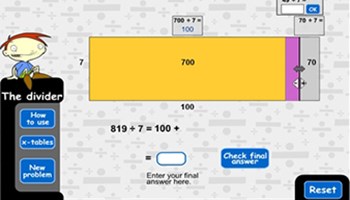
The divider: with or without remainders
Use this interactive game to solve division problems with and without a remainder.
Go to resource -
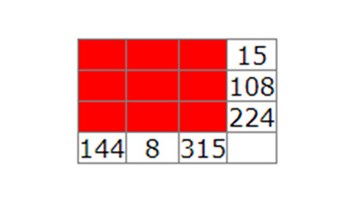
Multiplication squares
This problem requires learners to find common factors and offers a context in which they can explain their reasoning.
Go to resource -
Multiple multiplication methods
In this lesson students focus on using place value, tidy numbers, and doubling and halving strategies to solve multiplication problems.
Go to resource -
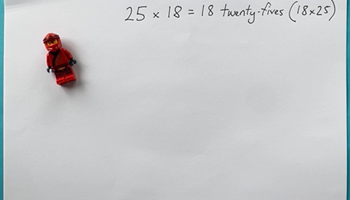
How would you solve 25 x 18?
Use this video to discuss efficient strategies to solve a two-digit multiplication problem.
Go to resource -

Multiplication: 2 digit by 2 digit numbers: Video and teaching guide
Use this video to explore multiplicative strategies, methods and models to solve a given worded problem.
Go to resource
