Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M3N04
Numeracy Progression: Multiplicative strategies: P5
At this level, students further develop multiplication and division concepts. They multiply and divide one- and two-digit numbers. Students represent problems using number sentences, diagrams and arrays, and use a variety of calculation strategies.
Classroom talks enable students to collaboratively solve mathematical problems presented as a class. Through a typical number talk, students are presented with a problem or scenario and asked what they notice and wonder or how they might solve the particular problem.
Through the number talk, provide scenarios where students can form equal groups to count a collection, and explore the notion ‘groups of’ through the use of arrays by changing the collection's columns and rows.
Include a range of representations and strategies such as skip counting, fact families, doubling and repeated doubling, partitioning, compensation and use of commutativity, and building from known facts.
Teaching and learning summary:
- Use classroom talks to present situations that involve multiplicative thinking.
- Model, and prompt students to use, efficient strategies to solve multiplication and division problems.
- Connect number problems to multiplication and division problems.
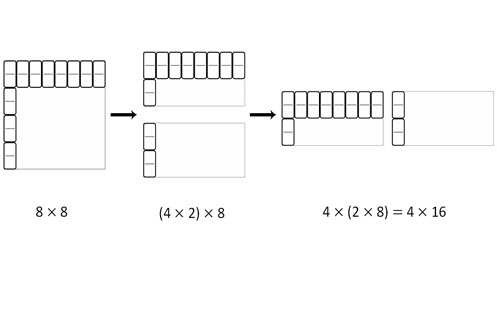
Students:
- develop increasingly efficient mental strategies to multiply and divide one- and two-digit numbers
- represent multiplication and division problems in different ways.
Some students may:
- get confused with the mathematical language used when discussing multiplication and division. To help students, model the use of mathematical language that focuses on the structure of the problem, such as ‘groups of’ or ‘shared between’.
- be inaccurate when displaying arrays of objects and have an imprecise pattern. They may have difficulties making a link between the array and what seems to be an abstract number amount.
- believe that they must multiply the numbers in the order that they are expressed as an equation. Explicit teaching of commutativity can help students appreciate how it can help them simplify and solve equations involving multiplication.
- be unsure or not understand what to do with the remainders when carrying out division. Help students recognise that what we do with remainders depends on the context. We can’t share 11 balloons evenly between 2 people but we can share 11 biscuits as we can break the eleventh biscuit in half.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning to recognise arrays in our world.
Why are we learning about this?
- Arrays are very useful for helping us build mental images of multiplication and division.
What to do
1. This egg carton is an example of an array.
- Can you see two rows of six?
- What else do you notice?
- Can you also see two groups of six?
- How many altogether?
- Write some maths equations that equal the number of eggs.

2. Go on an array hunt around your home.
- Draw a picture of an array that you found.
- Tell a story about your array that would enable someone else to draw it without seeing it.
Success criteria
I can:
- recognise arrays around me
- write maths equations for an array.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-
Classroom talks
Classroom talks enable students to develop language, build mathematical thinking skills and create mathematical meaning through collaborative conversations.
Go to resource -

Collaborative learning
For group work to be effective students need to be taught explicitly how to work together in different settings, such as pairs or larger groups, and they need to practise these skills.
Go to resource -

Concrete, Representational, Abstract (CRA model)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource -
Feedback
It has been shown that good feedback can make a significant difference to a student’s future performance.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

reSolve: Multiplication – domino arrays
This sequence of two lessons explores multiplicative thinking using arrays where all the parts of the array are not visible.
Go to resource -

Let us divide!
Each different scenario draws attention to a different way of thinking about the idea of division.
Go to resource -

What's going on? Properties of multiplication and division
This unit develops students’ recognition of pattern (consistency) in equations involving multiplication and division with whole numbers.
Go to resource -

Equal sharing using multiplication
In this lesson, students use their known multiplication facts to solve equal sharing problems.
Go to resource -

An apple a day
Students use arrays to solve multiplication facts.
Go to resource -

Selecting multiplication facts
Use this lesson to support students to select an appropriate multiplication fact to solve a problem with equal sets.
Go to resource -

Number facts: Multiplication and division
Use this guide to support students to develop fluency in automatic recall of number facts, an essential aspect of efficient mental computation.
Go to resource -

Times as many
Use this activity to support students in using their knowledge of multiplication basic facts to solve ‘times as many’ problems.
Go to resource -

Dot card talk 2
Students use their knowledge of arrays to solve problems.
Go to resource -

Times tables: 2, 4 and 8, and the relationship between them
Build up the four/eight times table using different interpretations of multiplication and division.
Go to resource -

Times tables: 3, 6 and 9, and the relationship between them
Build up the three/six/nine times table using different interpretations of multiplication and division.
Go to resource
Assessment
By the end of Year 3, students use mathematical modelling to solve practical problems involving single-digit multiplication and division, recalling multiplication facts for twos, threes, fours, fives and tens, and using a range of strategies.
-

Mathematics Year 3: ACARA
Use work sample 9, Number: Apple orchard to gauge students’ additive and multiplicative thinking.
Go to resource -

Ways to make 18
Use this task to assess students’ proficiency in applying additive strategies and multiplicative thinking to solve problems involving two- and three-digit numbers.
Go to resource