Year level: 4

Strand: Number, Algebra

Lesson length: 60 mins

In this first of three lessons, students use efficient strategies when performing calculations involving money. They explore different ways to estimate and calculate the distribution of pocket money.

Pocket money: Partitioning money amounts Image

Achievement standard

Students use their proficiency with addition and multiplication facts to add and subtract, multiply and divide numbers efficiently.

Content descriptions

Students develop efficient strategies and use appropriate digital tools for solving problems involving addition and subtraction, and multiplication and division where there is no remainder. AC9M4N06

Students recall and demonstrate proficiency with multiplication facts up to 10 x 10 and related division facts; extend and apply facts to develop efficient mental strategies for computation with larger numbers without a calculator. AC9M4A02

General capabilities

Numeracy

Critical and Creative Thinking

  • Analysing: Interpret concepts and problems Inquiring
  • Inquiring: Identify, Process and Evaluate information
  • Observe the working out in students’ workbooks during the reflection and make notes on what you have observed.
  • Listen to students’ explanations during the reflection.
  • Notice the level of difficulty based on the student’s choice of sharing, for example, equal amounts for each job or exploring the use of different amounts allocated to jobs performed.
  • Be familiar with the concept of pocket money
  • Estimation and approaches to making an estimate
  • Share dollar amounts in different ways

Some students may:

  • experience difficulties reading and understanding the learning task. There are many choices students can make in relation to the task, for example, amount of money selected to be shared, the ways the money is shared (equally, unequally), and the allocation of different values to the jobs performed
  • find it challenging to identify that there are multiple ways of partitioning numbers resulting in equal and/or unequal parts
  • require support to use efficient strategies to partition numbers into different sized parts
  • require support to use additive thinking to check solutions for accuracy, inverse relationship between addition and subtraction
  • find it challenging to make reasonable estimates for money amounts allocated to specific household jobs.

What you need:

  • Lesson plan (Word)

  • Teacher’s slides: efficient strategies (PowerPoint)

  • Teacher’s slides: classroom talk (PowerPoint)

Learning goals

Learning intention

We are learning to use efficient strategies when performing calculations involving money.

Success criteria

By the end of this lesson, students can:

  • show different ways to distribute money values
  • use efficient strategies when solving money problems
  • use their proficiency with addition and multiplication facts to add and subtract, multiply and divide numbers efficiently.

Why are we learning about this?

Working with money is an essential skill in life. From the beginning of primary school, we learn that there is an exchange process when we want to buy something. We also learn about needs and wants. It is important to understand the importance of spending, sharing and saving. As we move into our teens and then adult years, we experience handling our own money and make financial decisions based on our earnings and what we can afford.

Learning hook 10 mins

Download and use the teacher’s slides to accompany your teaching. You will find this in the ‘What you need’ section.

Introduction

  • Use the Teacher’s slides: classroom talk. Discuss What’s the same? What’s different?

Three arrays that equal twelve

Slide 1

  • Encourage students to think individually about these questions. Invite students to share their thinking. Use questioning and feedback to prompt students to notice that 12 is represented as an array in three different ways

Explicit teaching

  • If students do not make links to multiplicative thinking, use questioning and feedback, for example:
    • Say: The first image shows 12 split or shared into 2. There are 6 in each row.
    • Ask: What does the second image show? What connections can you make between the numbers in the bar model (the 12 and the number underneath it).
  • Show slide 2. Use this slide to discuss the three different ways 12 is shared.
  • If students refer to repeated addition only, prompt them to think of the numbers as ‘groups’. What is another way to share your thoughts about these images, using the word groups?

Differentiation (extension)

What are some other ways we can split or share 12 evenly? As this is an open question, it caters for different levels of ability.

Differentiation (support)

Use physical materials. Students model the 12 and then make the rows as shown in the picture. Encourage them to share what they notice is happening as they partition 12 into the rows.

Pocket money

  • Use the Teacher’s slides: efficient strategies to introduce the context of pocket money. Refer to Slide 2. Ask: What do you notice? What are you wondering?
  • Engage: the students with questions such as:
    • What types of jobs do you do at home? If you don’t do any, what could you help out with?
    • Do you believe you should receive pocket money for these jobs? Why or why not?
    • How much do you think you should receive for the various jobs you help with?
    • Do you share pocket money between your siblings?

Explicit teaching:

  • Make the learning intention and success criteria (Slide 3)
  • Explain that sometimes we need to partition amounts (collections) into equal groups and sometimes we can make unequal groups. Each action requires the total amount (collection) to be split/partitioned. If we were to put the parts back together again we would have the whole amount or collection again. Refer to the example in slide 4 demonstrating how 10 can be partitioned into equal and unequal groups.)

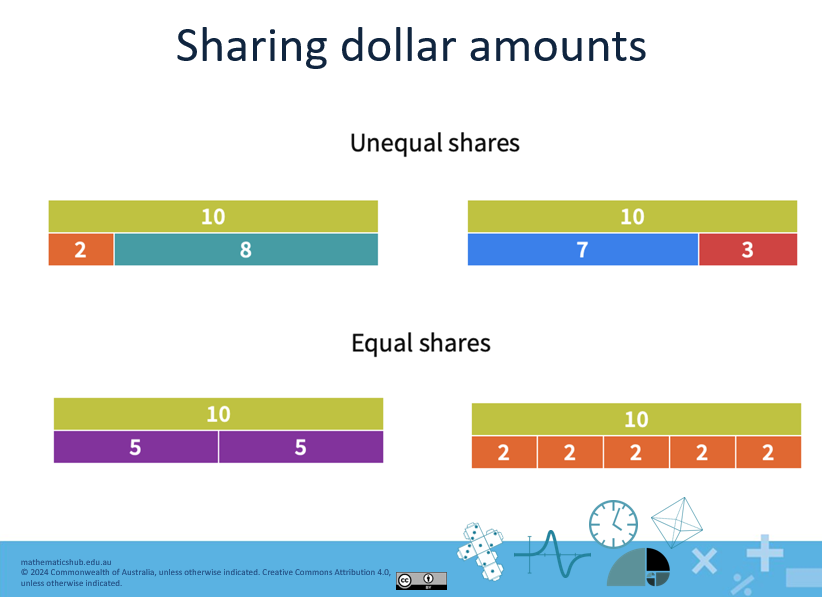
A slide showing four ways to work out a problem using a bar model. Ten is broken up into two and eight, Ten is broken up into three and seven. Ten is broken up into five and five. Ten is broken up into two and two and two and two and two.

Slide 4

  • In this lesson we will use the bar model to represent our mathematical ideas related to number sentences. We are investigating how the numbers in a sentence are connected to the situation. Sharing – diagram or array to show unknown, matching number sentence and strategy.
  • This lesson is in preparation for Pocket money: Mathematical modelling, which focuses on three children and the pocket money they receive for their jobs. Their parents decide that the children should come to an agreement about how the pocket money should be shared between them. The lesson guides students to use mathematical modelling to solve the problem.

Explore 40 mins

Sharing with equal amounts (division)

Continue to use the slides: Pocket money: efficient strategies to introduce sharing strategies. 

Explicit teaching

  • Explain: Division means splitting, sharing or partitioning an amount up into equal parts. When we share a collection of objects/things into equal parts, it is a fair share. The fair shares can be put back together again to form the whole collection.

Note: use the term you consistently use for division, while letting students know that there are other words that also mean the same action.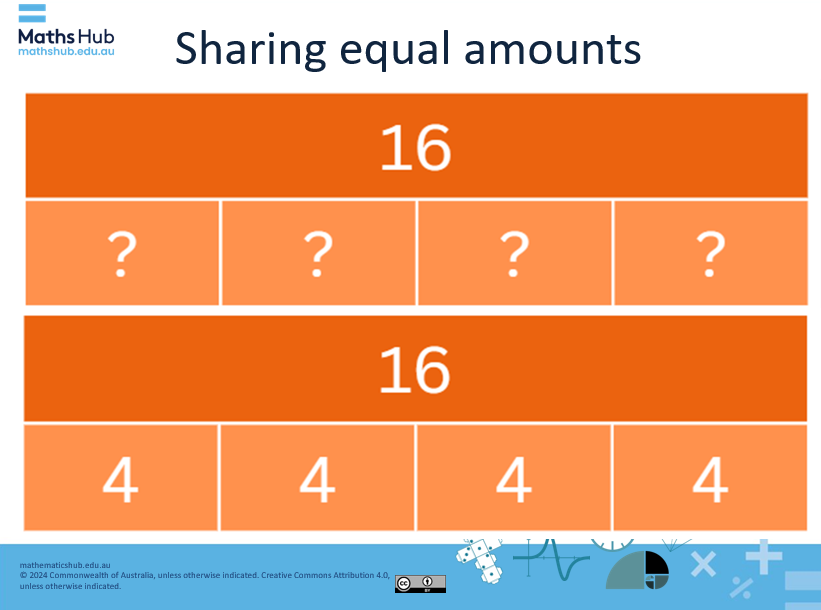Slide showing 16 broken up equally with four in each box of the box model.

Slide 5

      • Use the first part of slide 5 to present a problem and have students answer by completing their response on a mini-whiteboard, chalk board or other recording sheet. Follow up the question with the bar model representation.

        This is a bar model and represents the following:

        • 16 is shared equally between 4 parts. Each part has a value of 4.
        • 16 ÷ 4 = 4
      • Explain that we can also use bar models to share money amounts (slide 6). Say:

Let’s explore the number problem: 3 children shared $18 equally between them.

$18 does share equally between 3 parts (3 children). How much does each part (child) receive?

Slide showing 18 equally shared by three which is six.

Slide 6

  • Use additive thinking to share the money in unequal parts. Present a bar model that shows an amount in this case $12 shared unequally. Students use their additive thinking to explore the problem represented as a bar model of unequal parts.

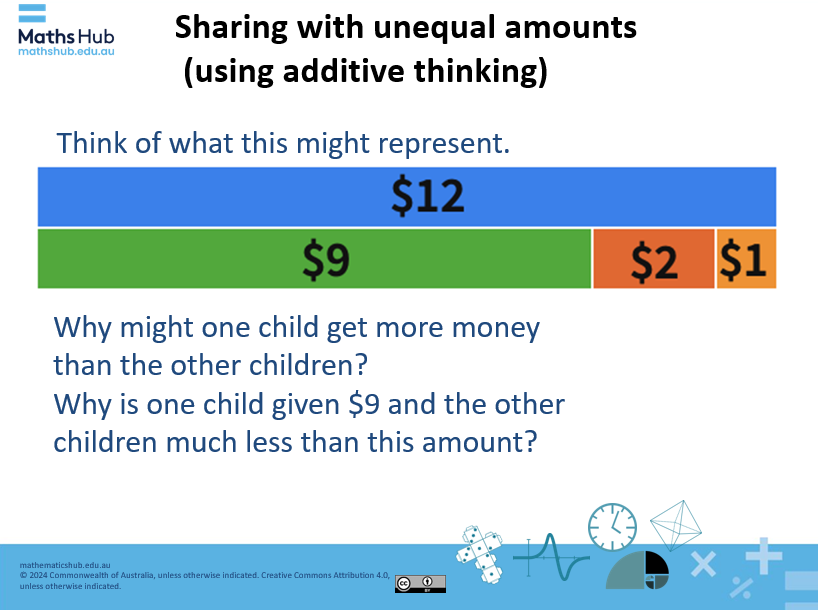
Slide showing twelve dollars divided unequally with nine, two and one dollar.

Slide 7

Differentiation (extension) 

Refer to slides 8–10.

  • Sometimes money amounts are shared in unequal parts. What if the children had been given $18 to share between them based on the type of jobs they do around the house. Some jobs require more time and effort than others therefore a child may be given more money than the others. How might we base the payment on an amount of time?

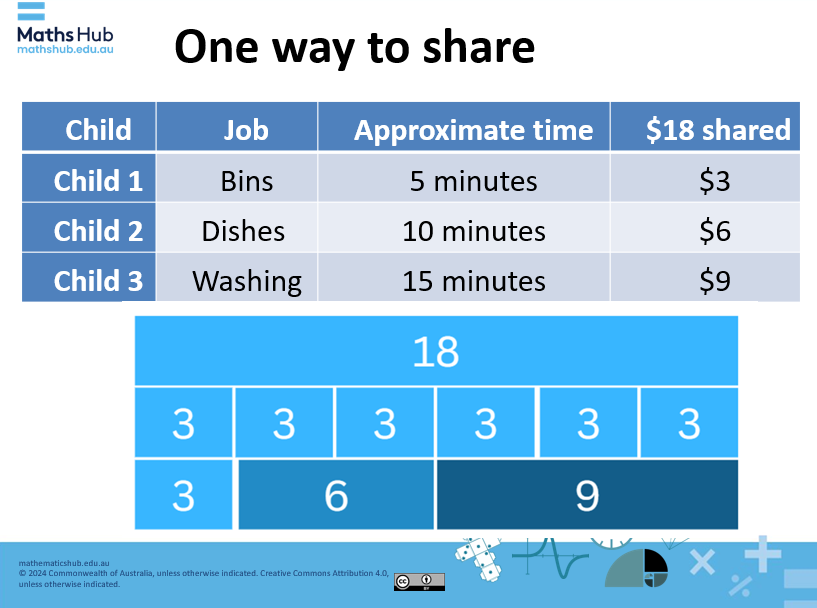
Slide showing jobs around the house and money values. A box model is shown representing eighteen dollars divided up into three, six and nine.

Slide 10

Learning Task #1 (slide 11)

What are some ways pocket money could be distributed, based on the jobs completed?

  • How much pocket money do you suggest should be distributed?
  • How many people is it shared between?
  • Will you have an equal or unequal distribution of money amounts for
    • each person
    • each job completed?
  • What type of jobs will you include?
  • How will you decide how much money is allocated for each job?

Think about how you can present your work so it is easy to interpret (read and understand).

Clearly show your working out for each step in the problem.

Enabling prompt: some examples

  • Encourage the use of equal distribution of money between two people to begin with.
  • Provide a written problem for the student to solve before moving onto the more open learning task. For example, share $12 shared between four people. Each person receives the same amount of money for the jobs they complete.
  • Provide the student with a table from the mini lesson to help guide their thinking.

A box model showing sixteen divided into four parts with a question mark in each box.

Extending prompt:

Encourage the distribution of money in dollar and cent amounts, for example, taking out the rubbish = $2.25.

Summary and reflection 10 mins

  • Share representations of number problems.
  • Ask students to share their thinking behind their choices of money distributions.
  • Ask students to share the maths they used to solve the problem.
  • Prompt students to discuss the way they used their knowledge of additive thinking to calculate and check their mathematics.