Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M8SP01, AC9M8SP02
Numeracy Progression: Understanding geometric properties: P7, Proportional thinking: P6
At this level, students begin to explore geometric properties and proof. They identify the properties of quadrilaterals based on transformation, angles, parallel sides, side lengths, diagonals and symmetry.
Students need to understand that congruence is more than similarity – ‘looking the same’. In a geometric context congruence means that two (or more) shapes are identical and that this can be tested (proven) by transforming one shape onto the other. Hence, students need to be familiar with transformations prior to starting this topic.
The topic of congruence is then extended to look specifically at the conditions for triangles to be congruent and to the properties of quadrilaterals. Students learn that if there is a correspondence between the shapes such that corresponding angles and sides are congruent, it means the shapes are congruent. There are three common ways to prove that two triangles are congruent:
![]()
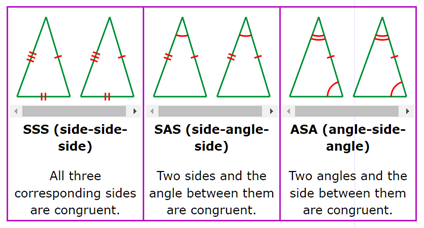
The fourth, is recognising congruency between right-angled triangles.
Students apply their knowledge of the properties of triangles and quadrilaterals to construct and design objects such as a toolbox.
Note: this is a large topic and will take time to cover in detail. It is advised to deliver it in more than one block.
The concept of proof will be explored in more depth in the following years when students explore Pythagoras’ theorem and trigonometry. Gaining a good understanding at this level will help them in future studies.
Teaching and learning summary:
- Revise the vocabulary of triangles and quadrilaterals.
- Revise previous knowledge of angles.
- Establish the notation and symbols used in geometric proof.
- Revise previous knowledge of transformations – rotation, translation, reflection.
- Discuss the conditions for congruence of plane shapes.
- Demonstrate the proofs of congruence for triangles – SSS, SAS, ASA, RHS.
- Identify the conditions for congruence to solve problems.
- Establish properties of quadrilaterals in relation to congruence and angles.
- Use and explain reasoning to solve problems about congruence.
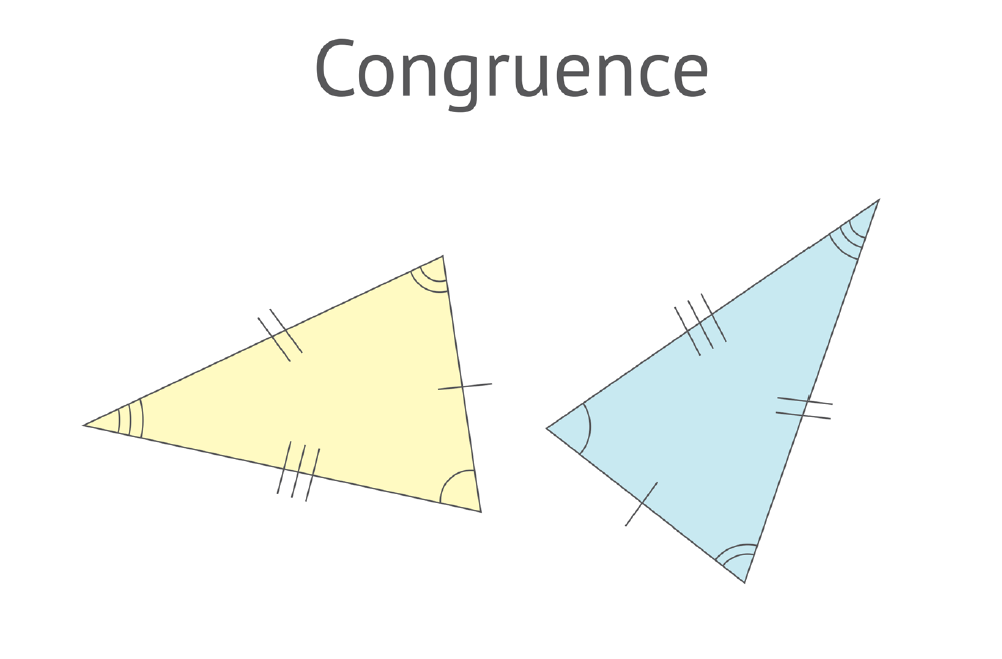
Students:
- define the conditions for two plane shapes to be congruent
- describe the transformation, or series of transformations, that maps one shape on top of another
- prove that two triangles are congruent, using the correct terminology and notation
- use the conditions of congruence to solve problems
- explain their reasoning in their approach to solving problems of congruence
- establish properties of quadrilaterals using geometric properties.
Some students may:
- confuse similarity with congruence.
- label diagrams incorrectly.
- confuse and misunderstand the meaning of the symbols used in geometry. (Show explicitly what each symbol represents and get students to practise them to develop confidence.)
- not show all the steps in a proof and require a lot of practice formulating sequences and logic.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- I am learning to define congruence of plane shapes using transformations.
- I will apply the four standard congruence tests for triangles.
- I will apply knowledge of congruence to solve problems.
Why are we learning about this?
Understanding congruence allows us to transform shapes. When an understanding of geometric properties is developed, we can apply this understanding to solving problems all around us; for example, designing and making a model of a house and then applying those plans to build a real house.
What to do
Complete the following interactive tasks that explore properties of geometric figures.
For each task, drag figures on the screen to discover angle and length measurements and to recognise and explore invariant properties.
On completion of each task, prepare notes to discuss your findings when back in class or online.
Task 1: Which shapes are congruent?
Open the interactive Are these shapes congruent?
- Determine which two shapes are congruent by moving each slider to the right.
- Define congruence of two shapes in your own words.
- Record all answers in your book and discuss.
Task 2: Congruent triangles
Open the interactive Congruent triangles.
- Demonstrate how you would make the two triangles congruent and give reasons for your answer.
Task 3: Congruent hexagons
Open the interactive Congruent hexagons
- Click and drag any blue point of the hexagons to vary the area.
- Record in your book what features are preserved in congruent figures.
Success criteria
- I can demonstrate congruence tests for triangles – SSS, SAS, ASA, RHS.
- I can define the conditions for two plane shapes to be congruent using knowledge of transformation – rotation, translation, reflection.
- I can apply knowledge of congruence to solve problems.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource -

Concrete, Representational, Abstract (CRA)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource -
Metacognitive strategies
Metacognitive skills are those that students need to be able to reflect on their own learning, set goals for themselves, monitor their progress and make improvements to move forward.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Making triangles
In this lesson, students investigate various combinations of three natural numbers to explore the concept of triangle inequality.
Go to resource -
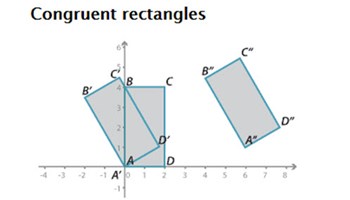
Congruence
This resource focuses on the definitions and proofs that two plane shapes are congruent. It gives detailed explanations of the curriculum content, worked examples and assessment questions.
Go to resource -

Congruence of plane figures
This resource explains the meaning of congruence and demonstrates the various proofs for triangles to be congruent.
Go to resource -
Mechanical linkages – Quadrilaterals
This unit focuses on investigating geometry, starting with real-life objects, then making working models and finally using pre-prepared dynamic geometry software.
Go to resource -
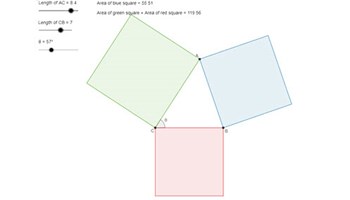
The Geometer’s warehouse: Stage 4 – Congruency
This resource consists of a series of activities that explore the conditions for two figures to be congruent.
Go to resource -
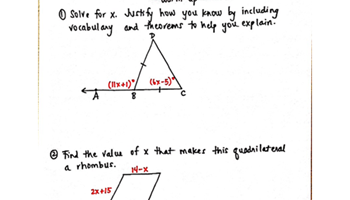
Discovering triangle congruence shortcuts
In this lesson sequence using construction, students will work in pairs to test ‘shortcuts’ to use when proving triangles are congruent.
Go to resource -
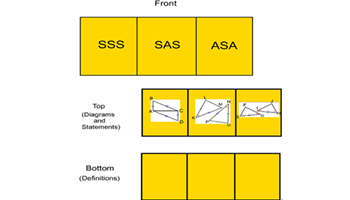
SSS, SAS, and ASA
Students create a graphic organiser to show the ways triangles are congruent. The hands-on activity gives students an opportunity to learn by 'doing'.
Go to resource