Mathematics investigation
Overview
At its core, mathematics is about problem-solving and modelling the world around us. By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding. Using a guided investigation model ensures that students stay focused on the mathematics being used and make connections to other areas of learning.
After students have been taught a skill or concept it is important that they apply it in a meaningful context as this will reveal the depth of their understanding. A guided inquiry is one way to do this. By scaffolding the problem, the teacher can lead students through a problem-solving exercise, highlighting the mathematics they need to use. Starting with a prompt – either a picture or a question – students can explore different ways of approaching the problem and communicating their thinking. Mathematics investigation links directly to the Critical and Creative Capability in the Australian Curriculum (Version 9.0).
Investigations can be differentiated by adjusting the complexity of the original problem or the expected outcomes. Investigations can be assessed and guided through the use of rubrics. A rubric for assessment is usually in the form of a matrix or grid. It is used to interpret and assess a student's work against identified criteria. A student can use the rubric to self-assess their own work.
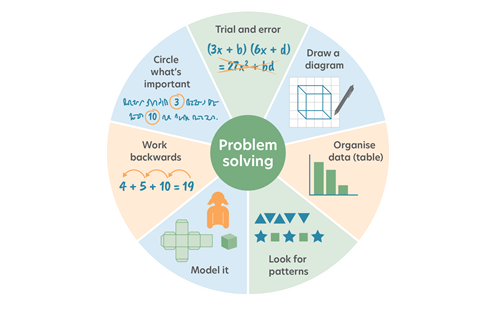
By using a particular scaffold or approach regularly, students learn what is expected of them and are able to improve and develop their problem-solving skills. Teachers should explicitly teach how to approach a problem using such a scaffold. Popular scaffolds or protocols for guided investigations include:
- reSolve
- Inquiry Maths
- Three-Act Tasks
To teach a Three-Act Task on the topic of ‘proportion and ratio’ include the following components, noting a Three-Act Task is a task consisting of three distinct sections.
- An engaging and perplexing Act One, often a video. Students discuss what they saw, pose questions and decide what information is needed for them to be able to answer the questions they have posed.
- An information and solution-seeking Act Two. Students are given the information they need and work, either in small groups or individually, to find a solution.
- A solution-discussion and revealing Act Three. Students discuss their findings and the solution is revealed. Students may then discuss and pose further questions.
The teacher:
- explicitly teaches the mathematics needed for the task
- explicitly teaches how to use a scaffold or protocol
- makes the learning intention and success criteria clear
- invites questions and wonderings
- focuses the students on the mathematical ideas being developed
- makes connections to students’ previous learning
- makes connections to other subject areas
- encourages students to work collaboratively
- monitors students, giving specific feedback to guide the students further.
The students:
- know how to use a particular scaffold or approach when working on a maths investigation to solve a problem
- know how to work collaboratively and respectfully
- communicate their ideas and thinking clearly
- ask questions and respectfully respond to other’s questions
- are prepared to struggle and make mistakes in order to make progress in their learning.
Examples of the strategy in action

In this video, a teacher discusses how they used an investigation to reinforce the students’ understanding of estimation and prediction.

A Three-Act Task on proportion and ratio.

The Inquiry Maths website showcases a model of guided inquiry that encourages students to apply their knowledge based on a given prompt.
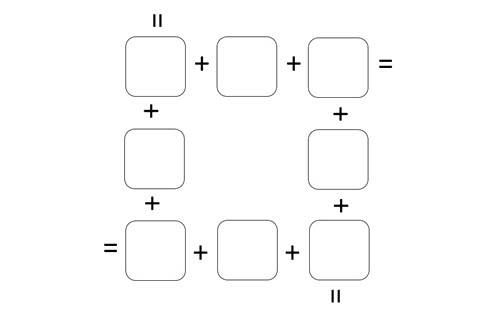
In an Open Middle problem an expression is presented and students are challenged to find the numbers that will make the expression true. They are challenging, suitable for all year levels, cover most maths topics, and promote problem-solving and reasoning skills. On this site you will find a comprehensive range of problems.

Transforming tasks strategy: from procedure to problem solving
Tasks are presented as following a ‘before and after’ approach. It demonstrates how to move from a procedural approach to posing questions that incorporate more of a problem-solving approach and mathematical investigation.