Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M7SP02
Numeracy Progression: Understanding geometric properties: P4
At this level, students build on their knowledge of two-dimensional shapes. They classify triangles according to their side length (scalene, isosceles, equilateral) and their angle properties (right, acute, obtuse). Students identify and describe different quadrilaterals (square, rectangle, parallelogram, rhombus, trapezium and kite) in terms of their side length, parallel edges and equal angles. Students also investigate the angle sum of a triangle and quadrilateral.
By presenting shapes in different forms and orientations, students will become familiar with their properties and be able to sort them accordingly. Encourage students to use the correct vocabulary and to be precise in their explanations. (This will help when they meet proof in Year 10.) Using physical objects and dynamic geometry software will also aid students in their visualisation.
Teaching and learning summary:
- Connect and build on students’ prior knowledge of triangles.
- Classify triangles according to their angles and side lengths.
- Connect to and build on students’ knowledge of quadrilaterals.
- Classify quadrilaterals according to their properties.
- Investigate the sum of the interior angles in a triangle and a quadrilateral.
- Demonstrate how to solve problems involving the angles in a triangle or quadrilateral.
Students:
- recognise and justify their classification of a triangle according to its angles and side lengths, using correct terminology
- recognise and justify their classification of a quadrilateral according to its properties, using the correct terminology
- know the sum of the interior angles in a triangle and quadrilateral and apply these facts to solve problems
- apply their knowledge of triangles, quadrilaterals and angles to solve problems
- explain their reasoning clearly when solving problems
- use estimation to ensure their solutions are sensible
- describe, sketch and draw two-dimensional shapes using conventional terms and notation specific to geometric properties.
Students may:
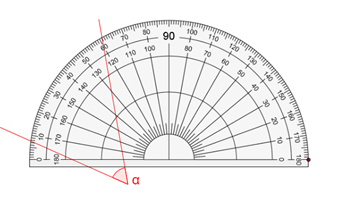
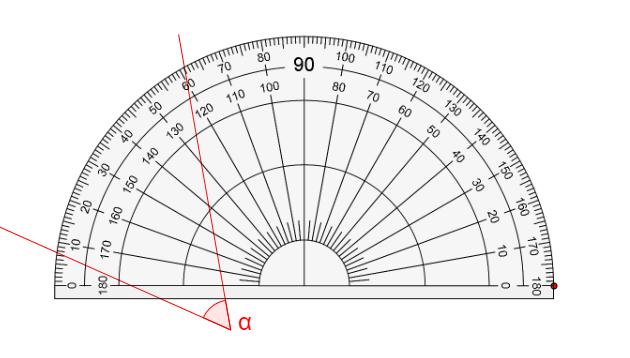
- confuse the upper and lower scale when measuring angles using a 180° protractor. Understanding basic angle properties such as acute and reflex angles helps with this.
- need explicit teaching and practical examples to understand that exterior angles in a polygon has to travel in the same direction for the sum to be 360°.
- not look at all the features of a shape when they are asked to classify it. Encourage students to look at all the sides and angles.
- struggle when the orientation of a shape is unusual. Students can turn the page to view the shape in a more ‘normal’ orientation.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning to recognise and justify the classification of triangles.
- We will recognise and justify the classification of quadrilaterals according to its properties.
- We will recognise the sum of interior angles in triangles and quadrilaterals.
- We can confidently explain our reasoning when solving problems.
Why are we learning about this?
It is important to confidently be able to classify triangles and to use this knowledge to assist in drawing two-dimensional shapes using the specific notation for geometric properties. By applying this knowledge, you can solve complex problems regarding triangles and quadrilaterals.
What to do
Activity 1: Access Triangles with three common measures on your device.
- Compare and contrast various triangles (3 sides and 3 angles; 2 sides and 1 angle; 2 angles and 1 side).
- Draw a table in your book and record the similarities and differences of each triangle in each set.
- Explain and or show your reasoning for each set.
Activity 2: Access Drawing triangles on your device.
- Compare different triangles and give reasons for your answers.
- Draw triangles of various measurements and explain or show your reasoning.
Success criteria
- I can recognise and justify the classification of triangles.
- I can recognise and justify the classification of quadrilaterals according to its properties.
- I know the sum of interior angles in a triangles and a quadrilateral.
- I can confidently explain my reasoning when solving problems.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -
Differentiation
Differentiation involves teachers creating lessons that are accessible and challenging for all students.
Go to resource -
Feedback
It has been shown that good feedback can make a significant difference to a student’s future performance.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Making triangles
In this lesson, students investigate various combinations of three natural numbers to explore the concept of triangle inequality.
Go to resource -

Geometric patterns
In this lesson students use intuition and logic to establish the side and angle properties of triangles and special quadrilaterals.
Go to resource -

Celebrity quadrilaterals: algorithms
In this lesson students develop an understanding of how a decision tree algorithm works.
Go to resource -
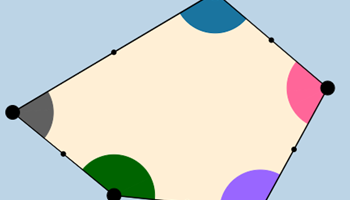
Finding the angle sum of any polygon
A series of activities that explore the angle sum of polygons using dynamic geometry software to explain and demonstrate the properties of the angles in triangles and quadrilaterals.
Go to resource -
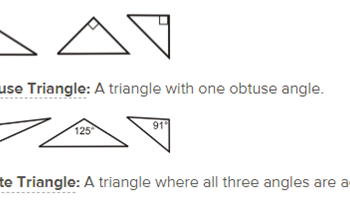
Classifying triangles
An explanation of how to classify triangles by looking at their angles and the lengths of their sides. The resource includes explanations, video, worked examples and questions.
Go to resource -
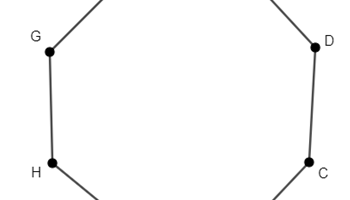
Sum of interior angles in a polygon
A series of student-based discovery activities that explore the sum of the interior angles of a polygon by deconstructing the polygons into triangles.
Go to resource -

Unit cubes and volume
Download this lesson plan that helps students to define and understand the concept of volume.
Go to resource