Celebrity quadrilaterals: algorithms

Curriculum information

Achievement standard

Students classify polygons according to their features and create an algorithm designed to sort and classify shapes. They represent objects two-dimensionally in different ways, describing the usefulness of these representations.

Content descriptions

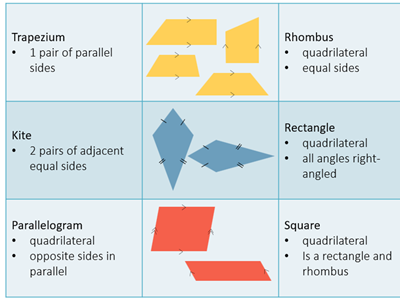
Students classify triangles, quadrilaterals and other polygons according to their side and angle properties; identify and reason about relationships. AC9M7SP02

Students design and create algorithms involving a sequence of steps and decisions that will sort and classify sets of shapes according to their attributes, and describe how the algorithms work. AC9M7SP04

General capabilities

Numeracy

Understanding geometric properties (Level 4)

Critical and Creative Thinking

Draw conclusions and provide reasons (Level 5)
Interpret concepts and problems (Level 5)
Draw conclusions and provide reasons (Level 5)
Create possibilities (Level 5)
Put ideas into action (Level 5)
Transfer knowledge (Level 5)

Assessment

The following opportunities for assessment are described below.

Use the Observational checklist of students describing, testing and refining their decision tree algorithms to assess if the students have achieved the success criteria. Decision algorithms can be submitted to teacher at the end of the lesson.
A digital submission could be a photo of their group’s decision tree algorithm and a brief reflection summary describing how their algorithm works.
Differentiation: Quadrilateral properties quiz using the Quadrilaterals worksheet. This would require another 50 minutes of class time to complete.

Prerequisite student knowledge and language

Key terms for this lesson: polygon, two-dimensional, algorithm, quadrilateral, parallel, parallelogram, trapezium, rhombus, convex, non-convex.

Areas of challenge

Some students may:

have only encountered one orientation of a plane shape, for example, on a poster in the classroom where only regular pentagons are displayed. Provide examples of different orientations.
not realise that classification of polygons is inclusive, for example a square is also a rectangle.

Suggested strategies

Using games and storybooks

Collaborative learning

What you need:

Lesson plan (Word)

Teacher's slides (PowerPoint)

Quadrilaterals worksheet (Word)

Rulers, coloured pencils, markers (or whiteboard markers)

A3 paper (or whiteboards)

Learning goals

Learning intention

We are learning to establish the properties of quadrilaterals using the side, angle and diagonal properties.
We will develop and refine a decision tree algorithm to classify special quadrilaterals by these properties.

Success criteria

By the end of this lesson, students can:

work collaboratively to develop a decision tree algorithm
classify special quadrilaterals by their properties
describe how their algorithm works.

Why are we learning about this?

Each plane shape has a precise meaning in geometry and therefore a standard definition. Knowledge of shapes and their properties leads to understanding around spatial relationships. It develops critical thinking skills, visual spatial reasoning and pattern recognition and can be applied to real-world skills like graphical skills, design and engineering. By developing an algorithm to classify shapes, students develop a foundational understanding of how machine learning can distinguish objects or images from each other.

Learning hook 10 mins

Note that, sequentially, it is suggested that the lesson: Geometric patterns is completed prior to this one, or go to Try these triangles: Assessment tasks by AAMT Top Drawer teachers, and print and hand out the PDF for students to complete. Enable students by also providing them with the Classifying triangles information sheet.

Use the accompanying teacher’s slides to present this lesson. Edit it to fit your class. Gather your resources before the lesson starts: A3 butcher’s paper/whiteboards, markers, pencils and rulers.

Introduction

Introduce students to the lesson by explaining that they will use game design to explore the properties of quadrilaterals (slide 1).
Students will play a modified game of ‘Celebrity heads’ to help develop a conceptual understanding of how an algorithm works to classify quadrilaterals. They will use their reasoning and problem-solving skills to create algorithms as part of a computational thinking process to ‘win’ the game.This game can be modified for classifying triangles or other polygons.
Display the learning intentions (slide 2) and outline the lesson.
Go to slide 3 and talk about the game they are about to play: ‘Celebrity quadrilaterals’. Explain that this game will help them to classify quadrilaterals by their special properties. Ask them what a quadrilateral is; if they don’t respond, define the term. Suggestion: ‘A quadrilateral is a polygon with four sides. Some quadrilaterals can have two classifications, for example, a square is also a rectangle, a parallelogram and a rhombus. In this game we will classify our quadrilaterals and corresponding celebrity name by the most applicable description.’
Ask for three volunteers to sit on three chairs at the front of the classroom, facing the class, with their back to the board or a wall. On the board behind them and above their heads (or on cards on the wall), write the names of three different special quadrilaterals from the slide (one per student).
The three volunteers ask the class yes/no questions to assist them in identifying the quadrilateral behind them. If the response to their question is ‘yes’, the student gets another turn. If the response is ‘no’, the next player asks a question. The three students are to remain seated until all quadrilaterals have been identified.
Repeat the task using two special quadrilaterals and one non-convex dart (arrowhead) quadrilateral. (Slide 4; refer to or use Convex and non-convex polygons: Information sheet.)

Draw different orientations of the quadrilaterals on the board too, so they look ‘different’, to address misunderstandings. The game can be played a third time if desired.

Explore 40 mins

Refer to slides 5–7. Students work in groups of two or three; give each group a copy of the Quadrilaterals worksheet. They will require an A3 sheet of paper and coloured pencils, or a whiteboard and marker, to work on collaboratively.
Explain to students that they will use the same line of questioning used in the celebrity shape game to identify and name quadrilaterals, but this time they create an algorithmic decision tree designed to classify quadrilaterals. Encourage a brief discussion here. Pose questions:
- How many yes/no questions do you need to ask to guarantee you know your quadrilateral?
- What would you ask first?
- If the class says ‘yes’, what would you ask next?
- If the class says ‘no’, what would you ask next?
Provide an example of what a decision tree looks like. An example of a triangle classification algorithm is shown on slides 6 and 7. The Quadrilateral worksheet offers a printable version of the quadrilaterals table and decision tree example.
Give students 20–40 minutes to develop a decision tree algorithm.
Once the algorithms are starting to come together, tell the class that it is important to test the algorithm against all possible classifications.
Ask students to pair up with another group of students to test their algorithm for all the ‘celebrity’ quadrilaterals from the worksheet.
Students are then asked to refine their algorithm based on the feedback.