Planning tool

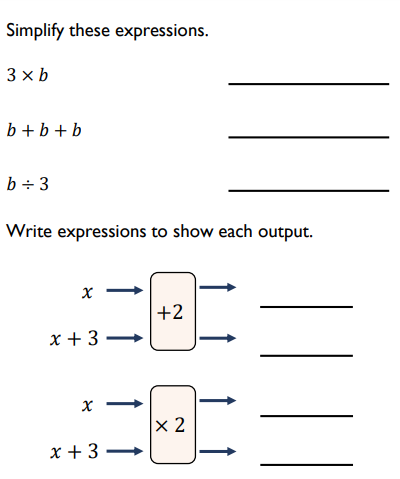
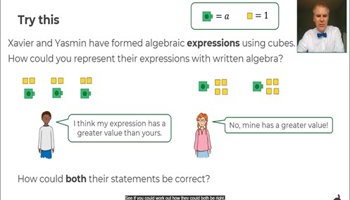
Students will:

• write an expression or equation from a word problem using pronumerals
• substitute a value for a pronumeral into an expression (or formula)
• manipulate pronumerals in expressions mathematically.

Some students may:

• not comprehend that letters stand for a specific amount or unit of measurement – use the term ‘pronumeral’ to emphasise that it means ‘a number’,
• confuse the variable x with the multiplication symbol – explain that therefore we ‘drop’ the multiplication symbol.
• not realise that equations must be balanced.

The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.

Learning intention

• We are learning how to substitute values into formulas.
• We are learning what happens when we alter the value of variables.

Why are we learning about this?

Our lives are full of choices. Some do not matter all that much, but some matter a lot. We can use mathematics to predict what will happen if we change our initial decisions, to make sure we make the right choice for the outcome we desire. When planning to build a house, it is important to select the right dimensions for each room to make sure it is tall enough for us to walk in but also large enough to fit the necessary furniture and fittings.

What to do

Hint: Area of a rectangle = length x width.

1. Grab any long, straight stick you can find in your garden, the bush or at the park. Your goal is to split it into four smaller sticks so that you can arrange them into a rectangle that encloses the largest possible area. That means you need to create the largest possible space inside the rectangle. 
2. How long should you make your pieces?
3. Measure your stick in centimetres (for example, 262 cm – I got lucky and found a giant stick!).
4. Halve this number, because you need two lengths and two widths to make an enclosed rectangle.
   (In this example, that’s 131 cm.)
5. Create a spreadsheet to explore all the possible combinations of length and width measurements you could have in your rectangle. Follow the example below.
6. Locate the maximum area value. You could use a formula for this such as =max(D2:D131).
7. Try this a few times with different sticks. What patterns do can you find? Can you draw any general conclusions about the best way to split up the stick?

Extension task: Design your playroom

Your neighbours have finished building their new house and have 45 m of timber left over. They offer it to you so you can build a room in your garden. Your task is to choose what are the most appropriate dimensions for this room so you don't cut the timber to the wrong lengths! You will need to consider whether you prioritise length, width, height or a balance of all three. You are limited to a rectangular design.

There is a formula we will use for this task:

Total timber required = (4 × length) + (4 × width) + (4 × height)

This is because we are making a 3D room, which has 12 edges in total. Try to locate them on the diagram below.

Let’s try an example:

Width = 6m

Length = 7m

Height = 3m 

Now we substitute these values into our formula.

Total timber required:

= (4 × 6m) + (4 × 7m) + (4 × 3m)

= 24m + 28m + 12m

= 64 m

Uh-oh. That’s not going to work. We only have 45 m of timber for this project.

• Can you find a set of dimensions that will work for this project?
• How much space (volume) will there be inside your room?
  Remember: Volume = length × width × height for a rectangular prism.
• Which set of dimensions will produce the largest possible volume?

Success criteria

• I can substitute values into formulas to solve problems algebraically.
• I can understand that when values of variables are altered a pattern emerges.