Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M6N02
Numeracy Progression: Multiplicative strategies: P7
At this level, students learn to decompose composites into their prime factors and recognise primes as the building blocks of composite numbers. Students consolidate use of the distributive and commutative laws of multiplication to simplify calculations.
To build relational understanding, encourage students to make concrete and symbolic representations of numbers and ask students to describe their properties. For example, represent square numbers using counters or square tiles. Introduce and connect symbolic notation, for example, 3 x 3 = 32, and explore patterns.
Highlight how identifying factors can be used to simplify calculations. For example, 15 x 16 can be simplified into 5 x 3 x 4 x 4 and rearranged to 5 x 4 x 3 x 4 = 240 to make the calculation easier. The rearranging of these numbers contextualises the commutative and distributive properties of multiplication.
Build on the students’ existing strategies to locate factors and highlight students’ attempts at using a systematic approach. Use these as the basis to explicitly teach efficient strategies, such as modelling the use of a tree diagram to find the ‘prime factors’ of a given number through ‘prime factorisation’.
Build a shared understanding of the following terms:
- prime numbers: a whole number higher than 1 that is only divisible by itself and 1
- composite numbers: a whole number that is divisible by numbers other than itself and 1, for example, 4 is divisible by 2 as well as 1 and itself
- square numbers: numbers that are the product of a number which is multiplied by itself, for example, 3 x 3, which can be written as 32
- prime factors: the smallest possible factors of a number (that are also prime numbers), for example, the prime factors of 20 are 2 x 2 x 5.
Make explicit the value of using division to distinguish between prime and composite numbers. Dynamic software such as an interactive hundreds chart can help students see and describe patterns and determine rules for numbers with certain factors.
Provide opportunities to explore complex problems, such as: ‘What are all the numbers which have up to 3 factors?’ Encourage systematic thinking, such as trial and error, using combinations of only the first three prime numbers, actively notice patterns that emerge, and use these observations to make and test conjectures.
Teaching and learning summary:
- Provide investigative opportunities to explore properties of prime, square and composite numbers.
- Provide repeated opportunities to make sense of, simplify and solve multiplication problems.
- Present open-ended problem-solving opportunities where systematic thinking and strategies such as trial and error are required.

Students:
- identify and describe numbers as prime and composite numbers, and provide reasoning
- explain and express the characteristics of square numbers
- express a number as a product of its prime factors
- use known factors to flexibly solve multiplicative problems.
Some students may:
- incorrectly apply the distributive law when multiplying two or more numbers. For example, if multiplying 15 x 16, a common misconception is to multiply the tens (10 x 10) and then multiply the ones (5 x 6). To address this, encourage students to model the equation using an array to help them recognise why this strategy doesn’t work. Use explicit teaching when useful.
- make errors in their calculations. To address this, encourage students to solve the problem using multiple methods and notice whether the answer is the same in all instances. Another useful strategy is to ask students to estimate the total before calculating. Both approaches can help the student make sense of the multiplicative situation, recognise unrealistic solutions and resolve the problem themselves.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention:
- We are learning to investigate prime, square and composite numbers.
Why are we learning about this?
- Some numbers have special properties. These properties can be used to solve problems. For example, we use base 60 for our system of time instead of base 10.
What to do
- Open this interactive tool, Sieve of Eratosthenes. It shows the first 100 numbers arranged in a 10 x 10 grid called a hundreds chart.
Have a go at one of the following investigations.
- Explore using the Sieve of Eratosthenes tool. List the prime numbers found in the first 100 numbers. How does the Sieve of Eratosthenes help you identify prime numbers?
- Some numbers are highly composite, meaning that they have a lot of factors. Locate some of these on the hundreds chart.
- Some of the prime numbers under 100 can be written as the sum of two square numbers. How many can you find?
- There are more prime numbers in the first 50 numbers than there are in the next 50 numbers. True or false?
Success criteria:
I can:
- identify numbers as prime or composite numbers and explain why they are prime or not
- identify square numbers and be able to explain to others what characteristics make it a square number.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Concrete, Representational, Abstract (CRA model)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource -
Multiple exposures
Providing students with multiple opportunities within different contexts to practise skills and apply concepts allows them to consolidate and deepen their understanding.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Factors bingo
In this lesson we use the context of a bingo game to apply understanding of prime, composite and square numbers.
Go to resource -

Two primes make one square
Use this task to spark curiosity about and explore properties of prime and square numbers.
Go to resource -
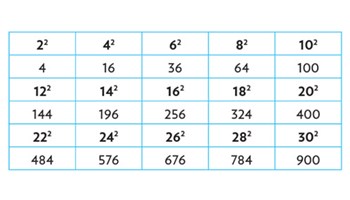
Scrutinising square numbers
Use this open-ended challenge to connect and apply important number properties.
Go to resource -

Primes and emirps
This activity is focused on exploring prime numbers.
Go to resource -
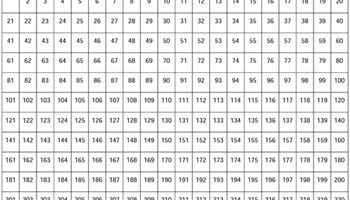
Sieve of Eratosthenes
Use this task to investigate properties of multiples and see the connections between primes and multiples.
Go to resource -

GeoGebra: Sieve of Eratosthenes
Use this dynamic software to explore prime and composite numbers to 100.
Go to resource -
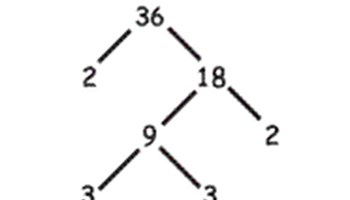
How many factors?
This activity is focused on finding factors of numbers.
Go to resource -

Mathigon Polypad: Prime Factor Circles
Dynamic software that students can use in tandem with the Prime Factor Circles lesson.
Go to resource