Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M7N01, AC9M7N02
Numeracy Progression: Multiplicative strategies: P9
At this level, students explore, investigate and describe the relationship between square numbers and square roots.
By making connections to visual representations, such as a square dot diagram, students visualise the relationship of inverse operations and how it could apply to area diagrams. It is vital to cement the connection between the term 'squared' and side lengths of a square.
Begin with a line in 1D (one dimensional) of length X, turn it into a 2D square with area X2, and then into 3D to make a cube with volume X3. Demonstrate perimeter and area of squares and square roots, labelling diagrams alongside number problems. Use the inverse square root to work backwards to find the length of a square.
The distributive property will help students work further with BIDMAS (Brackets, Indices, Division, Multiplication, Addition, Subtraction), showing students that there is more than one way to solve problems. Students now learn that they are using indices; therefore, a set of ‘order of operations’ questions should be interleaved.
Allow students to work mathematically to investigate lists of square numbers. Develop skills to recognise number patterns and investigate the development of pattern rules. Use a visual sequence for students to explore how a power series increases; that a new row and column are added to the diagram, with one being of equal length to the previous and the other being n + 1.
Use number lines of square numbers to predict and make estimations of non-perfect square values; for example, 43 is between the square numbers 36 and 49 so √43 is between √36 and √49 and therefore between 6 and 7.
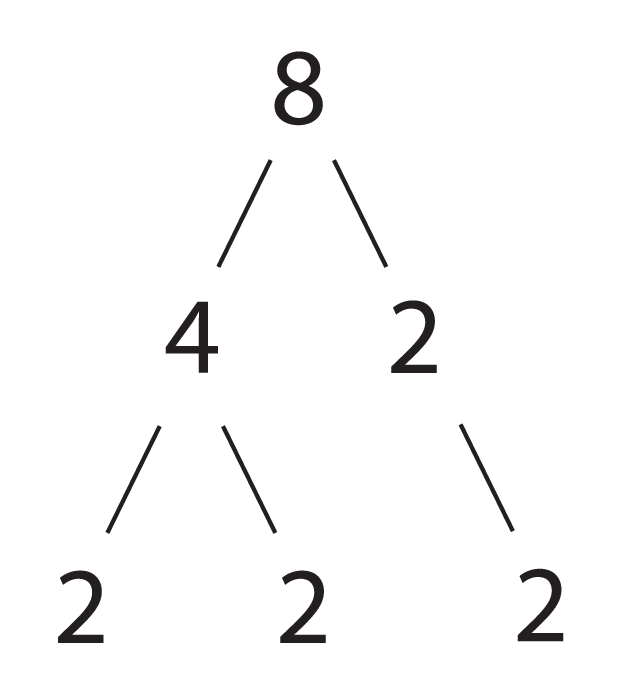
Students extend their understanding to include index notation and products of prime numbers, deepening understanding that numbers can be represented in multiple ways. Students see the importance of prime numbers as the building blocks of the number system, and that there are many patterns and facts about primes that can be explored. Prime factorisation can be presented as the discovery of the unique building blocks of each number.
Students explore and develop fluency with factors, multiples, HCF (highest common factor) and LCM (lowest common multiple). Review the concepts of prime and composite numbers and ensure students can define and compare these differences. Illustrate how any number can be written as a product of its prime factors and that this can be used to find the HCF and LCM. Use these representations to solve problems.
Teaching and learning summary:
- Investigate squares of natural numbers from 1 to 20. Make visual connections using dot square patterns.
- Review factors, multiples, HCF and LCM.
- Describe the relationship between square and square roots and use the distributive property and area diagrams to calculate two-digit numbers.
- Estimate an imperfect square root on a number line of consecutive squares by comparing it to the size of natural squares.
- Create lists of squares to identify patterns and make predictions.
- Find the perimeter of squares using square numbers. Work backwards by using the inverse.
- Introduce index notation as an alternative way to represent a number.
- Introduce the product of prime numbers as an alternative way to represent a number, and prime numbers as building blocks.
- Introduce and develop index notation, and sequences of powers of 2, 3 and 5.
- Explain how these concepts can be used to find the LCM and HCF (useful when simplifying fractions).
- Represent numbers in expanded form and powers of 10.
Students:
- understand that numbers can be represented in a variety of formats
- identify multiples and factors, including all factor pairs of a number, and common factors of two numbers
- understand the terms ‘composite’ and ‘prime’ and recognise such numbers
- are able to express a number as a product of its primes
- find the square and square root of a number
- calculate the squares of two-digit numbers
- are familiar with index notation and its vocabulary
- are able to express whole numbers in exponent notation for powers of 10.
Some students may:
- require extensive revision of factors and multiples.
- need additional explicit instruction to integrate indices into their understanding of order of operations (BIDMAS).
- misinterpret x2 as 2 times x instead of x times x.
- confuse the terms ‘square’ and ‘square root’ and have difficulty in seeing the same number as having two different meanings.
- confuse the terms ‘factor’ and ‘multiple’.
- incorrectly identify 1 as a prime (it is not as it only has one factor) and 2 as not a prime number (it is the only even prime).
- misunderstand that adding two different multiples of the same number results in another multiple of that number.
- confuse the square as relating to perimeter rather than area.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- I will list all the factors of a number.
- I will calculate squares of natural numbers and square roots.
- I will break a number down into its prime building blocks.
Why are we learning about this?
Have you ever wondered what all the fuss is about with prime numbers? There’s a good reason for this fuss. Not only do prime numbers keep us safe online with encryption, they also are the hidden blocks that all numbers are built from. It’s impossible to really understand numbers without spotting the primes lurking beneath them. But that’s not all. Numbers are full of patterns and surprises. Sometimes a number can represent an entire shape. Square numbers are the first step along another fascinating path. This skill is all about witnessing the beauty and hidden secrets of numbers.
What to do
It’s your lucky day. You have a perfect excuse to add a packet of M&M’s, Smarties, Skittles or another of your favourite small round lollies to the shopping list. Tell Mum and Dad ‘I need it for my maths homework!’ That’s the truth.
Squares
- Pour out a pile of lollies onto the table. But no eating yet! We’ve got some patterns to spot first.
- Arrange some of the pile into a square. Note down the number of lollies you used. You’ve now made a square number. How many lollies in each row? That tells you which square number it is.
- Try to increase the size of the square to the next natural size. This is the next square number.
- How many different squares could you make with 144 lollies? Do you notice a connection with the times tables?
- Use a table to organise your findings. Here’s an example:
| Number of lollies used | Lollies per row | Therefore | And |
| 25 | 5 | 52 = 25 | √25 = 5 |
We’re done with squares now! But if you want to explore more shapes, see what you can learn about triangular numbers with your pile of lollies.
Triangular numbers
- Take a handful of lollies and count them. Note down the number. I’ve got 32.
- Arrange your lollies into any sized rectangle. I could make a rectangle with 16 rows and 2 columns (or vice versa) or 4 rows and 8 columns (or vice versa) or 32 rows and 1 column (or vice versa). I've put my possibilities in the table below.
- If you can only make a rectangle with a single column/row, you’ve got a prime number of lollies. The different possible sides of the rectangles tell you the factors of the number you selected.
| Number | Rectangles | Factors |
| 32 | 16 × 2 8 × 4 32 × 1 |
1, 2, 4, 8, 16, 32 |
Go further
- Choose one of the possible rectangles for your number and repeat the following process for each of the side lengths. But you can’t choose the rectangle with only one row/column.
In my example I would arrange the numbers 4 and 8 into their own rectangles. Now I have two rectangles: 2 × 2 and 4 × 2. - Keep repeating these steps for any of the side lengths that can be arranged into new rectangles (without a single column/row of course – otherwise we will be here till the end of time on an endless loop!).
Now I have another 2 × 2. My final (prime) rectangles for the number 32 are 2 × 2 and 2 × 2. - You have found the prime factors of the number you started with.
Mine are 2, 2, 2, and 2. Or more simply: 24 - Experiment with a range of starting numbers and add an extra column to your table to organise your findings.
| Number | Rectangles | Factors | Prime factors |
| 32 | 16 × 2 8 × 4 32 × 1 |
1, 2, 4, 8, 16, 32 | 24 |
I bet you’ve built up an appetite (and probably snacked a little along the way). Now the lollies have been in your hands, I guess you need to eat them all.
Success criteria
I can:
- list the factors and prime factors for a given number
- calculate squares and square roots with small natural numbers.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Concrete, Representational, Abstract (CRA model)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -
Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Primes and prime factorisation
This module is for teachers who wish to consolidate their content knowledge on the topic of prime numbers and prime factorisation. There are sections on the history, the context and exercises, as well as examples on how to present and explain the concepts to students.
Go to resource -
Square roots and square numbers
This is a set of worked examples followed by a series of similar questions for the students to practise.
Go to resource -
Properties of number
This resource focuses on factors, multiples and prime factors. It also looks at how to apply these principles when using fractions. There is an informative video on how to present this material to students, and the common misconceptions they may hold.
Go to resource -
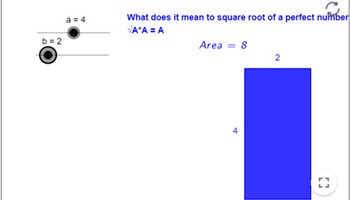
Square roots of a perfect number
This interactive visualisation shows students what it means to find the square root of a perfect number.
Go to resource -

Factors and multiples
To replace standard practice exercises with factors and multiples, students can pair up and play this game.
Go to resource
Assessment
By the end of Year 7, students can describe and understand the relationship between perfect square numbers and square roots, and can solve problems using the squares of numbers and the square roots of perfect squares.
-
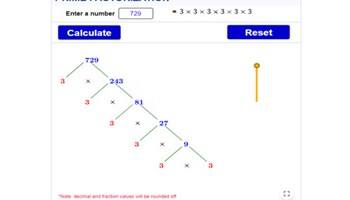
Prime factorisation
This interactive can be used as a formative assessment in class.
Go to resource -

Square and square roots
This is a quick online quiz that can assess how well a student grasps the concept of squares and square roots.
Go to resource -
Square roots on the number line
This formative assessment with answers allows students to connect visual squares with their square roots.
Go to resource