Year level: 6

Strand: Number

Lesson length: 60 mins

In this lesson we use the context of a bingo game to apply understanding of prime, composite and square numbers.

Factors bingo Image

Achievement standard

By the end of Year 6, students solve problems using the properties of prime, composite and square numbers.

Content descriptions

Students identify and describe the properties of prime, composite and square numbers and use these properties to solve problems and simplify calculations. AC9M6N02

General capabilities

Numeracy

  • Multiplicative strategies Level 9
  • Review student work samples from the challenge task to assess their proficiency with selecting numbers that are composite or square numbers.
  • Use slide 10 Exit ticket to record answers labelling the set of numbers provided as prime (P), composite (C) or square (Sq) or none of these (x).
  • Describe a composite number knowing that it is an integer divisible by smaller positive integers other than one and itself.
  • Describe a prime number knowing that it is an integer divisible by one and itself.
  • Describe a square number knowing that it is the result of multiplying a natural number by itself (for example, 9 is a square number as 3 x 3 = 9).
  • Use multiplication or division to test the properties of numbers.
  • Recall multiplication and related division facts to 10 x 10.
  • Be familiar with, and know how to play, the game bingo.

Terminology

Prime, composite and square numbers, factors

Some students may:

  • not understand commutative property of multiplication that the order of factors does not affect the product, for example, they may think that 6 × 3 and 3 × 6 are different numbers and not realise they result in the same product
  • confuse factors with multiples; factors of a number are the whole numbers that divide evenly into that number, multiplying factors together is the product. Multiples of a number are the products as a result of multiplying that number by other whole numbers. For example, the multiples of 5 are 5, 10, 15, 20, 25
  • not realise that a number might have more than one set of factors, for example, 24 has factors: 1 and 24, 2 and 12, 3 and 8, 4 and 6
  • believe that any even number is a square number.

What you need:

Learning goals

Learning intention

  • We are learning to understand the properties of prime, composite and square numbers.

Success criteria

By the end of this lesson, students can:

  • identify prime, composite and square numbers
  • use mathematical language to discuss properties of numbers (for example, positive integers, factors, multiples)
  • apply understanding of prime, composite and square numbers to solve a mathematical problem.

Why are we learning about this?

Understanding the properties of numbers will help in calculations, and develop an ability to simplify calculations through use of primes and squares. For example, simplifying 16 x 25 to its prime squares will give: 4 x 4 x 5 x 5. This can be rewritten as (4 x 5) x (4 x 5) to get (20) x (20).

Learning hook 15 mins

  • Download and use the teacher’s slides to accompany your teaching. You will find this in the ‘What you need’ section.
  • Begin with the learning intention and success criteria (provided on Slide 2). Unpack and discuss and key vocabulary and clarify students’ understanding.

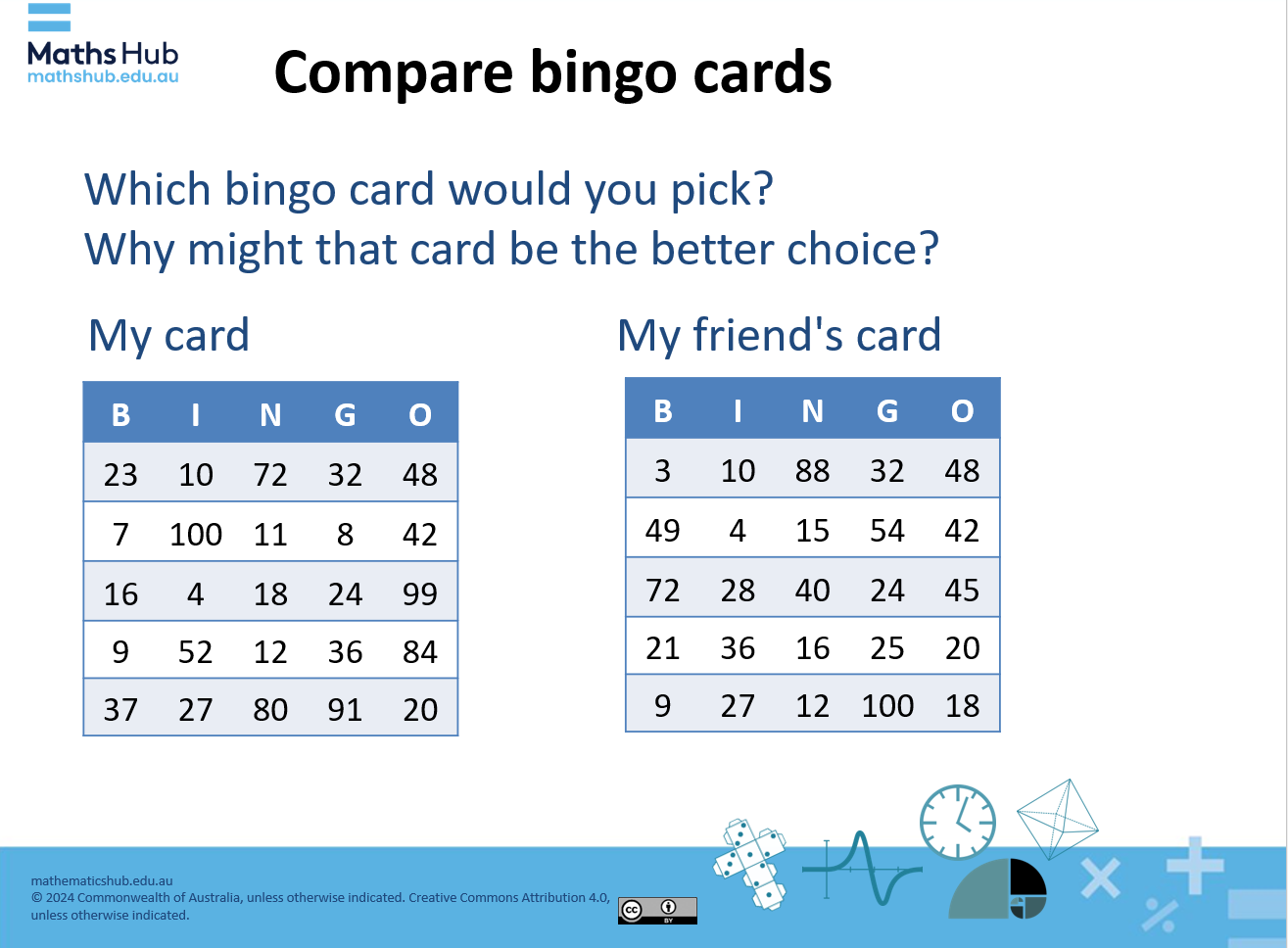
A slide showing two bingo cards with different numbers. Each card has 16 numbers. Text asks which card they would pick and why.

Slide 4

  • Use Slides 3-4 to introduce the task. The aim of this task if for students to recognise that numbers on the cards should include numbers that have multiple factors. They develop their understanding of composite numbers (those that have factors other than one and itself). By identifying numbers that cannot be rolled with two 10-sided dice they can identify numbers that are only divisible by one and itself (prime) numbers.
  • Use slides 6-8 to present the problem context to students. Read through the three discount options offered by each store. Allow time for students to clarify any questions they have.

Explicit teaching

  • Use slides 5-7 to assist students who require further support to engage and answer the challenge task on slide 4.

Differentiation

  • Support prompts: Which of the numbers will not be called? ​ How do you know? (Slide 5: Hint#1)
  • Enabling prompts:
    • List the factors of 16, 24, 19 and 8. Which of these numbers cannot be rolled with two 10-sided dice? (Slide 6: Hint#2)
    • How might a multiplication grid help you? (Slide 7: Hint#3)
  • Extending prompt: Is there a row that is likely to be completed first as a row? Why or why not?  

Explore 35 mins

Challenge task (Slide 8)

  • Students work individually or in pairs to design their own bingo card.
  • Ask students to explain how and why they selected the numbers they chose.
  • Ask students which numbers they didn’t include and why.
  • If time permits or in a follow up lesson have the students play factors bingo using the cards they designed.

Differentiation

  • Support prompt: What is a number that you would have on your bingo card? (Reduce the number of grids on the bingo card eg (2 x2 or 3 by 3).
  • Enabling prompt: What numbers are best to choose for your bingo card? What numbers will you not include?
  • Extending prompt: Which numbers have the highest chance of getting marked of first?

Summary and reflection 5 mins

  • Review definitions for prime, composite and square numbers.
  • Ask did knowing what prime, composite or square numbers are help you work out the task?