Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M5N02, AC9M5N06
Numeracy Progression: Multiplicative strategies: P6&7
At this level, students investigate the properties of multiplication as they learn increasingly efficient and sophisticated strategies to solve multiplication problems. They also explore divisibility rules.
Provide opportunities to connect concrete and symbolic representations of numbers and their factors. Invite students to create different array representations of a number with multiple factors using counters, for example, represent the number 12 with various arrays and record some arithmetic next to each example (e.g. 2 x 6, 3 x 4, 1 x 12). Ensure students can recognise and describe each number they explore in terms of its factors.
Challenge students to find all the ways a number can be partitioned using multiplication.
Dynamic software such as an interactive hundreds chart can help students see and describe patterns and determine rules for numbers with certain factors.
Ensure students are familiar with the properties of multiplication.
- Commutative property: changing the order of two factors does not affect the product. For example, 4 x 7 is the same as 7 x 4.
- Associative property: changing the order of three factors does not affect the product. For example, 2 x 5 x 7 is the same as 2 x 7 x 5. It is also the same as 5 x 2 x 7 and 7 x 2 x 5, and so on.
- Distributive property: decomposing (splitting) numbers in a multiplication problem and rearranging the order of factors does not affect the product. For example, make 7 x 8 easier to solve by breaking 7 into 5 and 2. So the problem then becomes (5 x 8) + (2 x 8), which is 40 + 16 = 56.
Use regular number talks that focus on breaking factors into smaller factors, and rearranging them, to create easier problems. For instance, to solve multiplication problems like 16 x 15, 16 can be thought of as 2 x 8 (that is, two of its factors are 2 and 8) and 15 can be thought of as 3 x 5 (having factors of 3 and 5). Therefore the problem can be rewritten as 2 x 8 x 3 x 5. Then rearrange the factors to make the calculation easier, for example, 2 x 5 = 10, 3 x 8 = 24 and, finally, 10 x 24 = 240.
Explicitly teach the doubling and halving strategy to help students find the factors of a given number. For example, 192 can be thought of as 1 x 192. Using doubling and halving you can create 2 x 96, 4 x 48, 8 x 24, 16 x 12, 32 x 6, 64 x 3.
Ensure students understand that all numbers generated are factors of 192. Once students are confident with doubling and halving, introduce other inverse relationships such as trebling and thirding.
Establish and encourage the use of key language including ‘factor’, ‘multiple’, ‘divisible’, ‘highest common factor’ and ‘lowest common factor’.
Teaching and learning summary:
- Provide repeated opportunities to make sense of and solve multiplication problems in different ways.
- Regularly emphasise doubling and halving and the area model as valuable strategies when solving certain multiplication.
Students:
- identify a number in terms of its factors and provide reasoning, for example, a number is divisible by its factors, so 2 and 5 are factors of 10 (in addition to 1 and 10, which are also factors of 10)
- understand and use the idea that changing the order of three factors does not affect the product (associative property), for example, 2 x 5 x 7 is the same as 2 x 7 x 5 and 5 x 2 x 7
- understand and use the idea that multiplication problems can be made easier by breaking factors into parts (distributive property), for example, 12 x 9 can be thought of as (10 x 9) + (2 x 9) = 90 + 18 = 108
- use doubling and halving strategies to solve some multiplication problems involving large numbers using, for example, 112 x 4 can be thought of as 224 x 2, and double 224 is 400 + 48, which is 448.
Some students may:
- incorrectly apply the distributive law when multiplying two or more numbers. For example, if multiplying 15 x 16, a common misconception is to multiply the 10s (10 x 10) and then multiply the 1s (5 x 6). Ask students to model the equation using an array to help them recognise why this strategy doesn’t work.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are developing strategies and confidence for multiplying larger numbers with a one-digit or two-digit number.
Why are we learning about this?
- Multiplication is used in all kinds of everyday situations and work situations.
What to do
Manipulating factors
- Challenge yourself to find other ways of solving a tricky multiplication problem. For instance, if someone struggled to remember 7 x 7, they could break one of the factors (7) up into parts (5 and 2) and work out (5 x 7) + (2 x 7) = 35 + 14 = 49.
- Over time, work with problems involving larger numbers, for example, 52 x 6 could be thought about as (52 x 3) + (52 x 3) = 156 + 156 = 312. Alternatively, 52 x 6 could be thought about as (50 x 6) + (2 x 6) = 300 + 12 = 312.
Doubling and halving
- Experiment with the doubling and halving strategy to see when it’s useful. This strategy involves doubling one factor in a multiplication problem and halving the other to help make the problem easier to solve. For instance, 50 x 8 can become 100 x 4, which is 400. Here’s another example: 25 x 14 can become 50 x 7, which is 350.
Success criteria
I can:
- use what I know about factors and number properties to make multiplication problems easier to solve
- experiment with strategies like doubling and halving to explore different ways of solving multiplication problems.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource -

Concrete, Representational, Abstract (CRA model)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -
Multiple exposures
Providing students with multiple opportunities within different contexts to practise skills and apply concepts allows them to consolidate and deepen their understanding.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
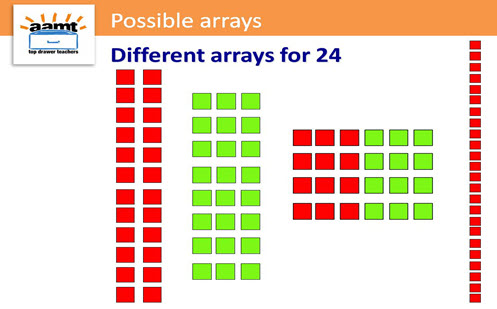
Arrays slide presentation
Use this slidedeck to discuss how many different arrays students can make to represent 24.
Go to resource -

Factors and multiples game
This game can replace standard practice exercises on finding factors and multiples.
Go to resource -
Sweets in a box
This investigation provides an engaging context in which to explore the factors of 36.
Go to resource -

Geared up
Students watch a short video of different-sized cogs interacting. This powers an investigation into common factors.
Go to resource -
Counting cogs
This problem reinforces and extends the thinking from the Geared up task, requiring students to think about factors and multiples.
Go to resource -
Divide and conquer
This activity focuses on using divisibility rules for 2, 3, and 5.
Go to resource -
Doubling and halving to find factors
The purpose of this activity is to support students in using doubling and halving to find the factors of a given number.
Go to resource -

Factors, multiples and primes
Use these teacher slides to explore factors, multiples and primes.
Go to resource
