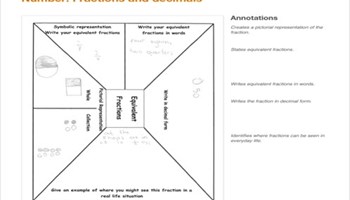
Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M4N03
Numeracy Progression: Interpreting fractions: P5
At this level, students continue working with the big idea of fraction equivalence and demonstrate their ability to express a part of a whole as being the same as other parts of a whole (e.g. 12 = 48 ).
Allow students to make and explore their own fraction families with a range of tasks using concrete materials. Paper-folding tasks will help students appreciate that when the number of parts increases, the size of each part decreases but the area remains the same (equivalence). Labelling each part also makes clear the denominator is the total number of parts and reinforces their understanding of proportional relationships as they see, for example, that 14 is half the size of 12 and
13 of the size of 34 .
Extend understanding of equivalence through encouraging students to demonstrate that when fractions are combined, they can be seen as being equivalent to a whole part
(e.g. 14 plus 12 ). Similarly, when fractions are partitioned, they can also be equivalent (e.g. splitting quarters in half gives eighths, and four of these eighths is the same as two-quarters, or one-half). Such ideas should be done with concrete materials.
Model correct mathematical language when describing the fractional parts to ensure that confusion does not arise between fractions and ordinal numbers (e.g. eighths and not eighth). When describing fractions, use terminology that recognises a fraction as one quantity and not two whole numbers. For example, 35 should be stated as ‘three-fifths’ not ‘3 over 5’. Place value language is also critical in helping students conceptualise decimal fractions. For example, 0.24 should be described as ‘two-tenths and four-hundredths’ or ‘24 hundredths’ rather than ‘zero point two four’.
Help students appreciate that decimal fractions can be thought of as simply another way of writing fractions. They are especially useful when thinking about place value ideas such as the multiplicative relationship between the places (‘ten of these is worth one of those’). Proportional models such as decipipes and decimats help students appreciate the relative size of decimal fractions. Encourage students to use and link language, visuals and symbols when interpreting decimal fractions.
Teaching and learning summary:
- Using a variety of concrete materials, guide students to find equivalent representations of related fractions.
- Demonstrate how fractions are related to decimals both visually (using decimats) and on a number line.
- Link fractions to decimals with reference to place value.
- Provide opportunities for students to use and link language, visuals and symbols to fractions and decimal fractions.
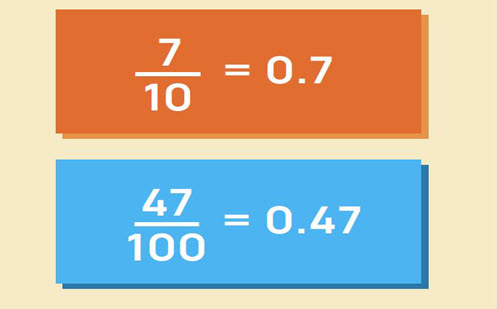
Students:
- find and represent equivalent fractions with related denominators
- show their understanding of the connections between fractions and decimals.
Some students may:
- be challenged when working with concepts associated with fractions. However, ideas of partitioning (sharing equally) and equivalence (different representations of the same amount) help student develop these concepts. Both improper and proper fractions can be seen as a number that lies between any two whole numbers.
- be confused between fractions and decimals. Address this by extending the idea that the number 1 can be partitioned into equal-sized parts and denotes a number between 0 and 1. Use a double number line with decimal numbers represented on one line and the fraction represented on the other. For example compare 0.5 and 34 . Using the double number line students should see that 34 is larger than 0.5. Other fractions can be formed and seen as numbers that lie between two whole numbers. In this approach mixed numbers can be introduced and represented on a number line.
- believe that a longer number is always larger. Students use whole-number thinking and think that 0.342 is larger than 0.4. Use number lines to compare the two numbers.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning to describe and represent decimal fractions using words, pictures and symbols.
Why are we learning about this?
- Decimals are part of our everyday lives.
What to do
1. Watch the video to learn how to make your game board.
2. Collect the resources you will need:
- 2 sheets of paper per player
- different coloured pencils or markers
- 1 spinner labelled tenths and hundredths
- 1 six-sided dice or 1–6 spinner (you could also use playing cards)
- 1 paperclip for the spinner
3. How to play
- Take turns to roll the dice and spin the spinner and fill in the game board.
For example: if you roll a 2 and spin ‘hundredths’, record your move as a fraction and as a decimal (0.02). - Colour in on the game board.
- Complete the What I filled column using words, for example, 'two-hundredths'.
- Calculate the total and record as a decimal.
- Use a different coloured marker or pen to fill in the game board for each turn.
- The winner is the first player to fill in 1-whole (their entire gameboard) or the player who’s gameboard is closest to 1-whole after 10 spins.
Success criteria
I can:
- describe and represent the decimal fraction that I rolled
- partition my decimal fraction to make it fit
- use place value language to describe my decimal fraction.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Concrete, Representational, Abstract (CRA model)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -
Multiple exposures
Providing students with multiple opportunities within different contexts to practise skills and apply concepts allows them to consolidate and deepen their understanding.
Go to resource -
Classroom talks
Classroom talks enable students to develop language, build mathematical thinking skills and create mathematical meaning through collaborative conversations.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Fruit fractions: Gardeners of fractions
In this lesson, students use a simulated garden bed to explore tenths.
Go to resource -
Fruit fractions: Fruit salad crafty creations
Students explore fractions through creating their very own simulated ‘fruit salad’.
Go to resource -

Fruit fractions: Growing with fruit
Explore fractions through plant growth in this engaging lesson.
Go to resource -
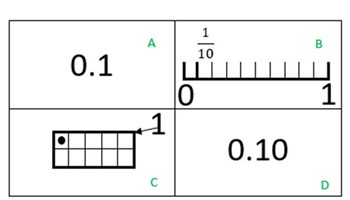
Measuring sticks: Decimals
In this lesson, students learn about place value and how it extends beyond whole numbers.
Go to resource -
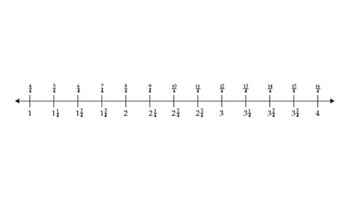
Fraction number lines
Students apply simple linear proportions to find equivalent fractions and order fractions.
Go to resource -
Decimals to tenths
This unit is an early introduction to decimals. Places are restricted to hundreds, tens, ones and tenths. Only addition and subtraction operations are used.
Go to resource -

Walking the rope
Students develop an understanding of the proportion and relationships between fractions.
Go to resource -

Half, more or less
A fun game for two or more players. Players take turns to create a fraction using playing cards, and determine where it fits in relation to a half.
Go to resource -
Unit: Equivalent fractions
This unit introduces students to equivalent fractions by investigating sets of fractions that represent the same value.
Go to resource -

Decimal fractions: Video and teaching guide
Use this video to explore decimal fractions, how they are represented and how we use them in day-to-day contexts.
Go to resource