Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M3N02
Numeracy Progression: Interpreting fractions: P5
At this level, students will develop their understanding of multiple representations of fractions including 12 , 13 , 14 , 15 and 16 using three different models: area models, length models and set models.
Area models are a useful starting point for the exploration of part-part-whole concepts, which include equal sharing and partitioning. Activities such as paper folding and the use of concrete materials, such as pattern blocks and fraction walls, can be used to scaffold thinking. Move beyond prototypical representations of fractions (typically, circular models) to support understanding. Additionally, provide opportunities for students to grapple with examples and non-examples (for example, ‘Which of these are equivalent to 14 ?') to challenge their thinking.
Length (or linear) models are based on relative length and are an important precursor to the use of fractional number lines in the future. The use of fraction strips (as seen in fraction walls), pieces of string, Unifix blocks and Cuisenaire rods are examples of length models which can be used to help students see fractional parts proportionally, enabling them to make comparisons and recognise equivalence. Online manipulative versions of Cuisenaire rods are also available.
Set models help students recognise the whole as a set of objects with the subsets making up the fractional parts. Concrete materials such as counters or similar items are useful in providing meaningful experiences of this form of thinking.
Multiple exposures using all three models reinforce students’ ability to visualise, estimate and make connections between these representations of fractions. To develop abstract thinking, encourage students to visualise fractions and describe what they pictured in their mind. See if their descriptions connect to the representations of the models explored.
Encourage mathematical reasoning by exploring non-prototypical examples of fractions and ask students to justify their thinking.
Model correct fractional language that will help students understand fractions as one quantity rather than two separate whole numbers. For example, describe 13 as ‘one third’ rather than ‘1 over 3’. In later years, use of this language will help students make sense of improper fractions such as 73 which should be described as ‘seven thirds’.
Students will need to be familiar with both quarters and fourths, as they will encounter both in everyday situations.
Teaching and learning summary:
- Use area, length and set models to represent unit fractions and their multiples.
- Combine fractions using repeated addition to make wholes.
- Use correct mathematical language when discussing fractions (not ‘over’).
Students:
- demonstrate their understanding of the relative size of common unit fractions
- demonstrate their knowledge of representing the whole 1 with unit fractions.
Some students may:
- believe that 45 is the same size as 56 as they both ‘have one piece missing’. This is often referred to as gap thinking. Use different representations and ask students to explain their thinking. Use questioning and feedback to address this.
- have an overreliance on set models which can reinforce the idea that fractions are two numbers rather than one (‘4 of the 5 squares are black’) which reminds them of their counting experiences with whole numbers. Area models are recommended for use until students’ understanding is strong enough to be able to interpret set models.
- experience difficulties with the concept of fractions because there is little understanding that equal parts are needed or because the process of naming the parts to provide the fraction name is not internalised. The use of a circular region as the mainstay of fraction teaching is often responsible for this, as the equality among the parts is not intuitively obvious to young children. The use of area or region models can help students develop an understanding of fractions that readily links to number lines.
- use whole-number ideas when working with fractions or they think of a fraction as two numbers: the numerator and the denominator. When they do not know what to do, they revert to thinking of only whole numbers. For example, they use the same reasoning as they do to order 2, 4, 6 and 8 to order the fractions 12 , 14 and 18 , without considering the size of each fraction. The use of benchmarking helps students make sense of fractions in relation to numbers such as 0, 12 and 1.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning to represent unit fractions in different ways.
Why are we learning about this?
We use fractions every day and it is important to understand how to draw and write fractions.
What to do
1. Find a sheet of paper. Fold it in half and then in half again. When you unfold it, you should be able to see quarters. Can you see how quarters and halves are in the same fraction family?
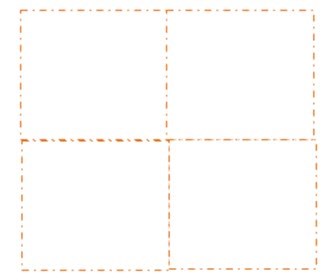
2. What other fractions and fraction families can you make by folding the paper in different ways?
3. Explain your thinking to a family member or friend.
4. Label and take a photo of the different fractions and fraction families that you have created.
Success criteria
I can:
- represent equivalent fractions.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -
Multiple exposures
Providing students with multiple opportunities within different contexts to practise skills and apply concepts allows them to consolidate and deepen their understanding.
Go to resource -

Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource -
Classroom talks
Classroom talks enable students to develop language, build mathematical thinking skills and create mathematical meaning through collaborative conversations.
Go to resource -

Concrete, Representational, Abstract (CRA model)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Fruit fractions: Fruit karate
In this lesson, students use fruit to explore common fractions.
Go to resource -

Fruit fractions: Gardeners of fractions
In this lesson, students use a simulated garden bed to explore tenths.
Go to resource -
Fruit fractions: Fruit salad crafty creations
Students explore fractions through creating their very own simulated ‘fruit salad’.
Go to resource -

Fruit fractions: Growing with fruit
Explore fractions through plant growth in this engaging lesson.
Go to resource -
Fruit fractions: Fruit kebab fun
In this lesson, we use fruit to explore common/decimal fractions relating to tenths.
Go to resource -

Fair feast
In this problem, the familiar context of sharing provides an opportunity in which to explore fractions in a variety of ways.
Go to resource -
Fraction matcher
Students match two representations of the same fraction. Eight levels of difficulty.
Go to resource -

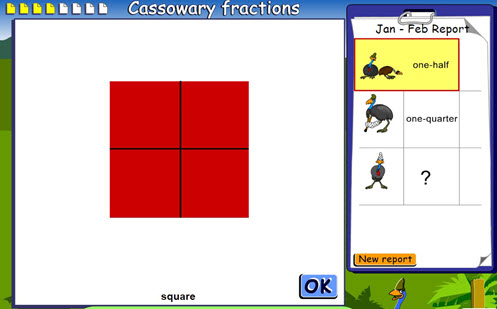
Cassowary fractions
Students design enclosures for cassowaries using simple shapes. They then divide the shapes into the given fractions to create separate pens. Immediate feedback is provided.
Go to resource -

Classroom talk: Fractions
Use this slide deck to run a number talk on fractions exploring equivalence, asking what is the same, what is different?
Go to resource -

reSolve: Authentic Problems: Bottle flipping
Bottle flipping is a popular game. Students decide what unit fraction of a bottle to fill with water to improve its chances of flipping easily.
Go to resource -
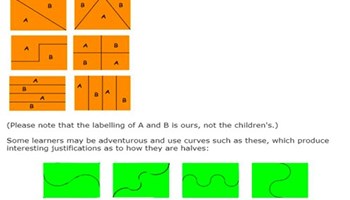
Paper halving
This task helps students recognise big fractional ideas such as equal sharing equivalence as they explore different ways to halve a piece of paper.
Go to resource -
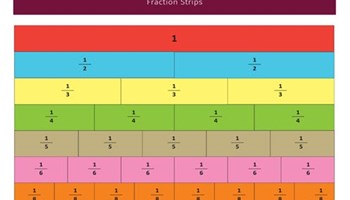
Equivalent fractions with sets
Use this unit to introduce students to equivalent fractions. Unlike whole numbers that occupy a unique position on the number line, there is an infinite set of fractions that represent the same value.
Go to resource -
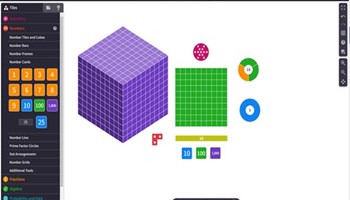
Mathigon: fractions
Use these virtual manipulatives to explore fractions.
Go to resource -
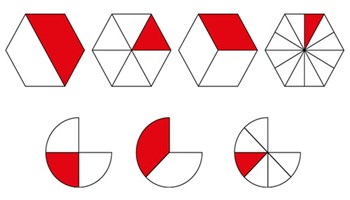
Unit fractions: identifying, representing and comparing
Recognise and show unit fractions of areas, lengths and quantities.
Go to resource