Fruit fractions: Fruit kebab fun

Use the teacher’s slides to complement your teaching. Pre-prepare your choice of materials needed for your class, such as the optional real fruit kebabs.

Warm-up challenge

Are these quarters? Prove It.

• Show image from slide 2. Students use mini-whiteboards or their exercise book to decide and prove whether the image shown is cut into quarters. Students justify their answer using mathematical language. ‘How can we prove it?’
• Expect responses such as: an inability to get started (may need to prompt with physical materials); misconception – students don't trust that half of a half is a quarter no matter what it looks like. Teacher uses concrete material (perhaps paper) to show that half of a half is a quarter, regardless of how it looks.

Differentiation (extension): How else could you have split a shape into 4 equivalent parts?

Differentiation (support): Use concrete materials; use a similar version involving halves rather than quarters.

Introduction

• Start the lesson by asking students if they've ever created or seen a colourful and delicious fruit kebab. (Show students a real-life example here with 10 pieces of fruit on it, if possible.)
• Do a ‘Classroom talk’ on various kebabs using the teacher's slides. For example:
  • Look at the strawberry and kiwi fruit kebab. What is the fraction of strawberries?
  • Do any fruit kebabs have half strawberry, half pineapple? How do you know?
• Display images on slide 3 showcasing various fruits, with a special focus on Aboriginal and Torres Strait Islander fruits such as quandong and finger limes. Prompt students to wonder about the taste and origin of these unique fruits. (Optional: A guest speaker with expert knowledge in this area could come in to discuss with the class.)
• Engage students with questions such as:
  • ‘What is your favourite type of fruit?’
  • ‘When might we want to create a fruit kebab?’
  • ‘How many pieces of fruit do you think we would fit on a fruit kebab?’

Explicit teaching: make the learning intentions and success criteria explicit. You can write them on the board or display them on a slide. Think, Pair, Share: students share with a buddy what they know about fractions and fruit kebabs. Explain, ‘Half means when something is divided into two equal parts, and you have just one of those parts.’

• Introduce the terms ‘numerator’ and ‘denominator’:

‘In the fraction   110, 10 is the denominator. It tells us the number of equal parts into which the whole is divided.’

Optional: Discuss the base 10 system: we have 10 fingers, our number system is based on 10. Ten-tenths make one whole, 10 ones make one ten.

‘The numerator is the top part of a fraction, representing the number of equal parts you have. For example, in the fraction   110, 1 is the numerator.’

Classroom talks: this lesson offers numerous opportunities for engaging conversations about when and how we use fractions to solve sharing problems.

• Instruct students that today they will be utilising coloured Unifix cubes to represent various pieces of fruit. Each kebab will have ten pieces of fruit on it (tenths). Use slides 4 and 5.
• Distribute coloured Unifix cubes with lots of various colours, for example, red for apple fractions and yellow for banana fractions.
• Instruct students to make half of their fruit kebab using red Unifix cubes (representing apple) and half using yellow Unifix cubes (representing banana).
• Act as a facilitator at the board, drawing and making connections between different student examples, observing ‘Do they all look the same or different?’.
• Instruct students to make different ‘fruit kebabs’ with various closed and open questions. For example:
  • make a fruit kebab with 5 red apples, then 5 bananas (closed)
  • make a fruit kebab with 5 red apples, and 2 other fruits (open).
• Students represent their fruit kebabs with written fractions.
• Help students to understand that unit fractions can be added together to make a whole.
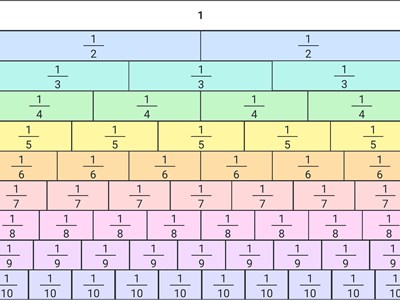
• Discuss equivalent fractions and introduce the concept of a 'fraction wall’. Show students the Fraction wall image on the next slide.
• Make connections between various equivalent fractions and the numerator or denominator, for example, 12   is greater than  4 10 . Just because you have four pieces doesn’t mean it’s necessarily more than one  piece. It depends on the size of the piece and what we have cut it into.
• Students draw/represent various fractions in their books or using a mini-whiteboards.

Differentiation (extension): Challenge students to incorporate patterns into their ‘fruit kebabs’; use more open-ended questions; introduce decimal notation.

Differentiation (support): Instead of working with tenths, work with quarters, or even halves. Use more closed questions (questions with only one correct answer).

CRA model: Use physical materials (concrete) that represent different pieces of fruit. Students begin by working with these tangible items, dividing a specific quantity into various unit fractions. This process helps them grasp the practicality of their starting number by observing the multiple ways it can be evenly divided. Illustrate fractions in ways that make sense to students (representational). Consequently, students can more easily develop a conceptual understanding of 'practical numbers' and express a number's 'practicality' through its factors (abstract).

Summarise the lesson's key points:

• Invite students to reflect on what they've learned.

Additional activity (10 minutes):

• If time allows, use playing cards to pull a card out and let that number represent the numerator for a piece of fruit on the kebab with tenths. For example, ‘If a 5 is drawn, that means it has 5 apples. What happens if we draw a number that means we have more than 10 tenths?’