Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M2N03
Numeracy Progression: Interpreting fractions: P2
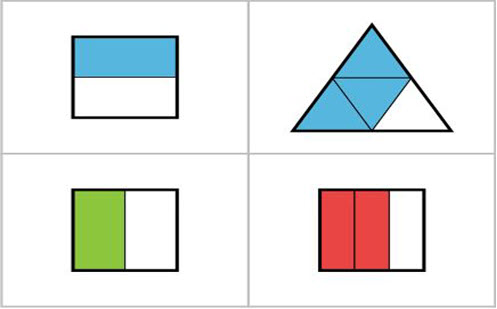
At this level, students are extending their knowledge and understanding of the meaning of half to include equivalent fractions (e.g. two-quarters and four-eighths). Students also extend their understanding of common uses of quarters and eighths, and other equivalent fractions.
Ensure that students understand the relationship between the number of parts and the size of the parts when developing their fraction sense. More specifically, students must realise that the more parts a quantity is divided into, the smaller each part must be. This is then linked to fractional language as ‘the larger the denominator, the smaller each part will be.’
Demonstrate the link between the denominator and the size of the fractional parts with physical models (e.g. fraction walls), and then demonstrate that fractions can be renamed. These renamed fractions are equivalent (the same size) even though the number of pieces may change. For example,
12 is equivalent to 48 , even though 48 has more pieces, the size of the fraction does not change.
Use a variety of models to develop students’ ability to visualise, estimate and create representations of fractions through partitioning different ‘wholes’. For example, the ‘whole’ can be shapes, strips of paper, pieces of string, or groups of objects. It is not advisable to only utilise pre-prepared representations of fractions (typically circular models) as this tends to encourage automatic and non-conceptual responses from students instead of encouraging them to think and visualise.
Extend student knowledge by providing them with opportunities to develop the understanding that with fraction models, the total area of the portion represented determines the size of the fraction modelled, and not the spatial arrangement. For example, in a circular model, the full circle is the ‘whole’ and the coloured section represents the fractional part.
Encourage students to investigate how fractions, as numbers, are both like and different from whole numbers. In order to prevent whole number thinking, it is important that teachers use correct mathematical language when discussing fractions (not positional language). For example, 12 should not be described as ‘one over two’.
Teaching and learning summary:
- Use a variety of models to develop an understanding of and demonstrate the relationship between halves, quarters, and eighths through repeated halving.
- Demonstrate links between the denominator and the size of fractional parts.
- Use correct mathematical language when describing fractions.
Students:
- recognise half as one equal part of one whole
- demonstrate their understanding of the connections between halves, quarters, and eighths.
Some students may:
- need help to see how fractions are alike and different from whole numbers. Direct students focus on the proportion of the model being indicated. Difficulties with the fraction concept usually occur because there is little understanding that equal parts are needed or because the process of naming the parts to provide the fraction name is not internalised. The use of a circular region as the mainstay of fraction teaching is often responsible for this, as the equality among the parts is not intuitively obvious to young children. Use area/region models to assist students in developing an understanding of fractions that readily links to number lines.
- use whole-number ideas when working with fractions or they think of a fraction as two numbers, the numerator and the denominator. When they do not know what to do, they revert to thinking of only whole numbers. For example, they use the same reasoning as they do to order 2, 4, 6 and 8 to order the fractions 12, 14 and 18 , without considering the size of each fraction. Students also need to be able to tell if a fraction is near 0 or near 1. They might see a fraction as a pair of whole numbers, for example, students might think that a fraction such as 14 is smaller than a fraction such as 18 because 4 is less than 8.
- think that the numerator and denominator are separate values and have difficulty seeing them as a single value. Use the number line to compare the relative sizes of numbers – there is always one more fraction to be found between two fractions.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning to connect basic fractions with everyday situations.
Why are we learning about this?
- To be able to see how fractional parts can be used in our day-to-day lives, and to develop a deeper understanding of the meaning of fractional language
What to do
- Here is an image of two equal sized chocolate bars. One bar has been cut into 8 pieces and the other cut into 4 pieces. You can only take 1 piece.

- Which would you choose? Why?
- Here is a pizza. How would you divide this up for four people?
- How much would each person get?
- Are the slices fair?

Success criteria
I can:
- use fractions to describe everyday situations.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource -

Concrete, Representational, Abstract (CRA model)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -
Classroom talks
Classroom talks enable students to develop language, build mathematical thinking skills and create mathematical meaning through collaborative conversations.
Go to resource -
Feedback
It has been shown that good feedback can make a significant difference to a student’s future performance.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
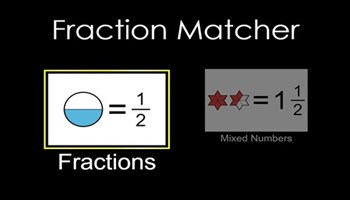
Fraction matcher
Students match two representations of the same fraction. Eight levels of difficulty.
Go to resource -

Sliced up
Use this three-act task to explore wholes and quarters.
Go to resource -

Fractions: paper folding
Students explore folding paper shapes into equal parts and labelling the parts with written fractions. A powerful way to help students explore equivalence and link visual and symbolic representations of common fractions.
Go to resource -

Getting partial
In this unit, students explore fractions of regions as well as fractions of sets. Students look for and develop understanding of the connection between fractions and division.
Go to resource -

Fraction bits and parts
Use this unit to make, name and recognise wholes, halves, thirds and quarters of a variety of objects.
Go to resource

