Expected level of development
Australian Curriculum Mathematics V9: AC9M5N05
Numeracy Progression: Interpreting fractions: P6
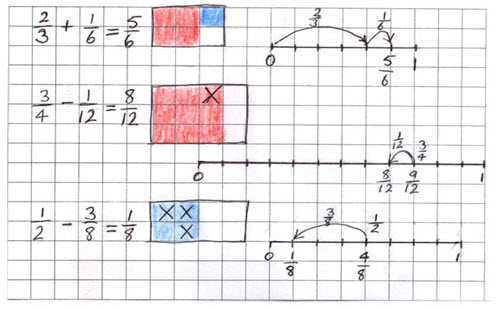
At this level, students utilise their understanding of the magnitude of fractions to add and subtract a variety of fractions. Students need to be able to understand fraction notation (e.g. the meaning of the numerator and denominator) and represent repeated addition and subtraction of simple fractions on number lines.
Use a range of models such as number lines, area/region models and abstract symbols to promote conceptual understanding. Number lines and the use of benchmark numbers can help students think about the relative magnitude of numbers, that is, they can see how 35 is closer to 12 than 1. Area/region models, such as a fraction wall, can help students solve problems like 16 + 13 by recognising 13 as equivalent to 26 and seeing that 16 + 26 = 36 which is equivalent to 12 . Demonstrate how questions like the one above can be checked using the inverse operation subtraction, 36 – 26 – 16 = 0.
Provide problems that require students to make meaning of the context rather than simply using computational methods. For example, ask students to make two fractions that are close to, but are not exactly 1. Ask students to justify the answers they obtain.
Develop flexible strategies for adding and subtracting fractions with related denominators by asking students to find two or more ways to solve problems such as 910 – 25 . A student may solve it one way using a computational method and another way using a number line jump strategy. This provides a context for the teacher to help students make connections between the different approaches, target common misconceptions and explicitly teach efficient strategies.
Continue to use correct mathematical language when describing the fractional parts to ensure that confusion does not arise between fractions and whole numbers (e.g. two-fifths, not two over five; two-fifths and four-fifths equals six-fifths).
Teaching and learning summary:
- Use a range of models to enable students to conceptualise addition and subtraction of fractions.
- Provide opportunities for students to make the link between fractions with related denominators, recognising equivalence.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning to represent fractions on the number using repeated addition.
Why are we learning about this?
- It is important to understand that fractions are not always less than 1.
Representing fractions on a number line helps us compare and make sense of quantities that exist between whole numbers.
What to do
1. Represent a fraction on a number line using repeated addition.
Look at this example, using 10 4 .
- 10 4 is 10 quarters and can be made by adding 64 and 44 .
2. Now use a number line to show how:
- 64 is the same as 14 + 14 + 14 + 14 + 14 + 14
- 44 is the same as 44 + 44 + 44 + 44 .
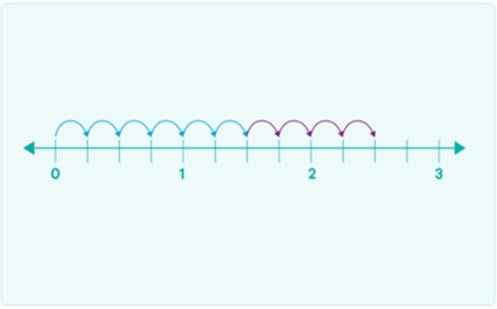
3. Use the number line and repeated addition to work out which of these fractions is larger.
a. 13 3 or 11 5
b. 10 4 or 15 6
c. 12 5 or 15 4
4. What other strategies can you use to determine which is the larger fraction?
Success criteria
I can:
- represent unit fractions on a number line
- show how to add and subtract fractions with the same denominator.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-
Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -
Concrete, Representational, Abstract (CRA model)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -
Classroom talks
Classroom talks enable students to develop language, build mathematical thinking skills and create mathematical meaning through collaborative conversations.
Go to resource -
Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource -
Feedback
It has been shown that good feedback can make a significant difference to a student’s future performance.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
Fraction shape puzzles
Students investigate fractions through the relationships between various shapes.
Go to resource -
Farm fence fractions
In this lesson, we explore fractions, decimals and perimeter.
Go to resource -
Cuisenaire rod fractions - Level 4
This unit introduces the idea that fractions come from equi-partitioning of one whole.
Go to resource -
Linked chains
Students build fluency and understanding as they add different combinations of fractions to be equivalent to a given number.
Go to resource -
Polypad: Fractions
Use these interactive tools for students to work with a range of mathematical ideas including fraction bars.
Go to resource -
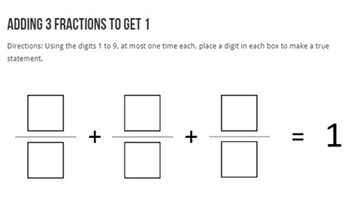
Adding fractions to get 1
A fluency-building open-ended task where students must use the digits 0 to 9, at most one time each, to fill in the boxes to make a true equation where the three fractions added together equal 1.
Go to resource -
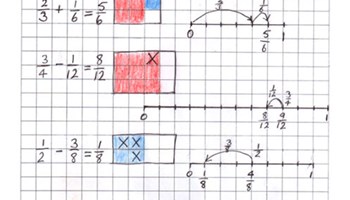
Grids and jumps
Explicit teaching ideas to help students make connections between symbolic, linear and area model representations of fractions.
Go to resource -
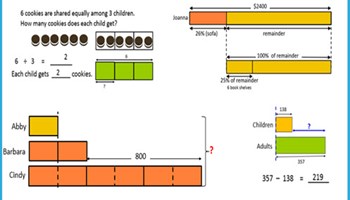
Bar model method: Introduction
This unit introduces students to two types of bar models for solving word problems: part-whole models and comparison models, each applied to addition, subtraction, multiplication and division.
Go to resource -
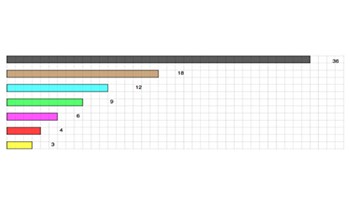
Fraction lengths
This activity involves addition of fractions with different denominators and mixed numbers, so that the concept of equivalent fractions is also explored.
Go to resource -
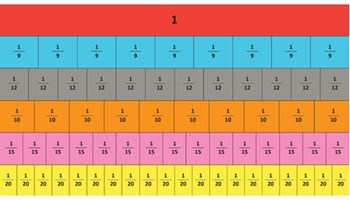
Getting partial to fractions
In this unit, students partition a length model into equal parts, to create unit fractions and add and subtract fractions.
Go to resource -
reSolve: Lamingtons
A series of lessons exploring the relationship between fractions and division.
Go to resource
Assessment
By the end of Year 5, students order and represent, add and subtract fractions with the same or related denominators.
-
Assessment: Equivalence and comparing fractions
Use this two-page resource to assess students' understanding of fractions, including equivalence and ordering fractions.
Go to resource -
Assessment: Adding fractions
Use this two-page resource to assess students' understanding of addition of fractions.
Go to resource