Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M6N05, AC9M6N03
Numeracy Progression: Interpreting fractions: P7
At this level, students develop increasingly efficient strategies for adding and subtracting fractions with related and unrelated denominators. They develop conceptual understanding by being given opportunities to estimate before computation and justify their thinking. They develop flexible strategies for solving problems using concrete, visual and pictorial representations.
Use questions like ‘approximately how much of the shape needs to be covered?’ and ‘approximately how far along the number line should this fraction go?’ to help students make sense of fractional quantities. Continue to promote number lines and benchmarks such as 14 , 12 and 34 to help students represent fractions and make comparisons between quantities.
Number lines can also be used to model addition and subtraction strategies, that is, using jump strategies as repeated addition. Where possible, link learning to realistic problems, for example, using part cups or spoons in a recipe or using the understanding of equivalent fractions.
Use physical materials such as pattern blocks, tangrams and Cuisenaire rods, or dynamic software such as interactive fraction walls, to facilitate learning of equivalent fractions and how they can be used to represent, add and subtract proper and improper fractions.
Extend intuitive ideas about halving numbers to extended fact families. For example, halving a piece of paper and halving again can be described as quartering. Repeated subtraction will illuminate eighths and sixteenths – other fractions in this fact family. Have students explore fact families that extend from thirding or fifthing.
Explicitly teach students how to add and subtract fractions with unrelated denominators by simplifying to the lowest common denominator. Link learning to their understanding of prime and composite numbers. To build conceptual understanding, encourage students to estimate a reasonable answer before calculating and use this to check and make sense of their solution.
Teaching and learning summary:
- Use understanding of fraction equivalence to solve problems involving addition and subtraction.
- Use a number line as a tool to represent, order, compare, add and subtract common fractions and recognise equivalence.
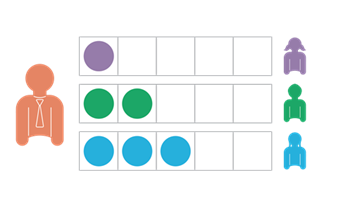
Students:
- demonstrate their understanding of fraction equivalence
- estimate reasonable answers and are able to justify their reasoning
- use diagrams and materials to build flexible strategies for adding and subtracting fractions.
Some students may:
- use whole-number thinking and believe that the fraction 15 is smaller than 110 because it has a smaller denominator. They may also see the numerator and the denominator as two separate whole numbers.
- see 34 and 56 as equivalent as they are both one number away from being a whole number. Model residual thinking where students compare the size of the fraction that is needed to get to 1( 14 and 16 ) to help them determine that there is a size difference between the two fractions.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning to add fractions with related and unrelated denominators.
Why are we learning about this?
- Understanding how fraction families work strengthens our understanding of fractions with related denominators and equivalence.
- Area models such as paper cut-outs are a powerful tool in helping us better understand fractional parts.
- Paper cut-outs can help us understand that while equivalent fractions must be the same size, they do not necessarily have to be the same shape.
What to do
- Find some pieces of A4 paper and a pair of scissors.
- Fold the paper in different ways to create some different sized fractions. For example, you can create 16 by halving and then thirding the paper.
- Label and cut out the different sized fractions you have made.
- Find one or more ways to make 1 by putting different combinations of the fractions back together.
Success criteria
I can:
- demonstrate an understanding of how to make 1 with different unit fractions
- create different shapes to represent the same fraction
- show how to add fractions with related and unrelated denominators.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource -
Classroom talks
Classroom talks enable students to develop language, build mathematical thinking skills and create mathematical meaning through collaborative conversations.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Farm fence fractions
In this lesson, we explore fractions, decimals and perimeter.
Go to resource -
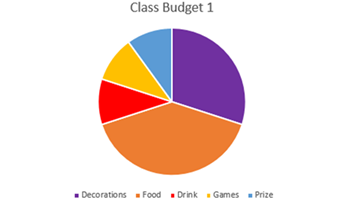
Fractional funds
Reinforce understanding of fractions in a practical context, by learning how to find a fraction or percentage of an amount, through budgeting.
Go to resource -

Tangrams 3 – reimagining wholes
An investigation of fraction parts represented as an area model in the form of tangrams. The original square made up of tangram pieces is worth 1 whole. What is the value of each of the other pieces?
Go to resource -

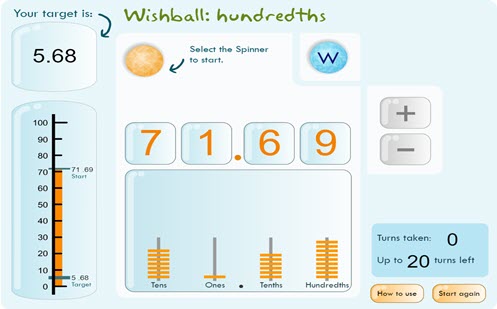
Wishball hundredths
Students use an interactive tool to test their understanding of decimal place value with numbers that include thousandths.
Go to resource -
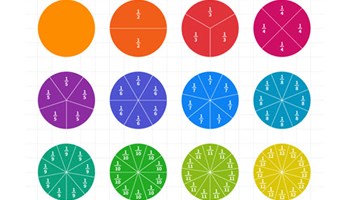
Mathigon fraction circles
Dynamic software that enables students to manipulate different-sized fractional pie pieces.
Go to resource -

Fraction of
Find a simple fraction of a quantity where the result is a whole number.
Go to resource -
reSolve: Fraction benchmarks
This sequence emphasises that fractions are numbers and develops students’ understanding of the relative size of fractions.
Go to resource -

Middle years maths challenges: Junior Chief Baker
Students work with quantities in a recipe to scale ingredients up or down to find the correct ratios. Refer to p 93 of the resource.
Go to resource -
Stripping fractions
This number activity focuses on adding and subtracting related fractions.
Go to resource
