Fractional funds

Warm-up challenge: Maths battle

• Show image from the Teacher’s slides (slide 2). Students use mini-whiteboards or their maths book to choose which student (Jordan or Taylor) is correct for the statement ‘Percentages are always out of 100’.

Expect responses that students agree with Jordan but have difficulty explaining why percentages are always out of 100.

Rate the responses: gather or annotate some students’ answers. Have a class discussion as to why percentages are always out of 100, relating to the language of ‘per cent’ and the two zeroes in the % symbol.

Set the content for investigation for a class party celebration. Ask students if they've ever been involved in planning a party and how they decided what to include and how much to spend.

• Show students slide 3, and facilitate a ‘Which one doesn’t belong’ discussion about the various class party budgets. (Note: There is no correct answer; this is an opportunity for students to share and develop their mathematical knowledge, language and justification.)
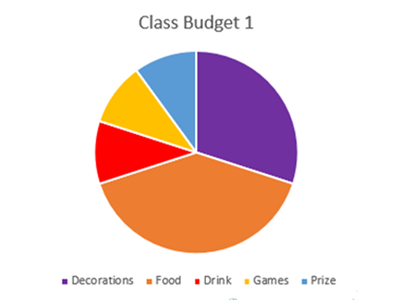
• Show slide 4, Looking at class party budget 1, and ask questions such as:
  • Which section has the largest budget?
  • Are there any sections that appear to have the same budget percentage?
  • What percentage or what fraction do you think each section represents?
  • Where and how do you think might use a pie chart in this way?
• Explain that today, they'll be taking on the role of party planners and budget managers. They have a fixed budget to organise a class party, and they need to make choices wisely.
• Have a class mind-map brainstorm about what things would need to be bought for a class party. List party expenses, such as decorations, food, drinks, games and prizes, and discuss the importance of budgeting for each of these categories.

Clarify that their goal is to create a successful party while staying within the budget. Discuss the real-world significance of budgeting and why it's an essential skill.

Introduction (5 mins)

• Learning intentions and success criteria: Display the learning intentions and success criteria (slides 5 and 6) for the lesson.

Worked examples: Sharing the whole (20 mins)

• Start by asking for two volunteers to come to the front of the class (or choose two students).
• Problem 1: Give the students 24 Unifix cubes or counters. Ask them to share them so that each student gets 12 . Ask the students what they divided them how they did, and how they knew that they each had half? Expect answers such as:
  • ‘I know that 12 of 24 is 12’: a response to this might be to ask the students ‘What would you do if there were 286 cubes/counters?’ to encourage them to articulate their strategy more generally.
  • ‘We made two equal piles’: this is important to understand that two halves have to be the same size.
  • ‘We divided the total by 2’: this is the key concept that you need the students to note, as when finding a fraction of an amount the first step is to divide the amount by the denominator. Use questions such as, ‘How did you divide the 24 cubes/counters up?’ and ‘How many groups did you need?’ to elicit this response.
  • Write 12 ,  12 on the board and circle it.
• Problem 2: Choose two different students and explain that this time we are not sharing the cubes/counters equally. Ask them to share them out so one student gets 12 and the other gets 34 . Ask the students what they did and how they knew that they had the right answer? Expect answers such as:
  • ‘We divided 24 by 4 which equals 6 and gave that to one person, the other person got the rest’: this is an important observation as it shows that the students understand that all the cubes/counters are being shared out and that 14 + 34 = 1.
  • ‘We divided the 24 cubes/counters into 4 equal piles, one person got one pile, the other got 3’: this thinking underpins the way of finding a fraction of an amount for non-unit fractions, for instance, first finding 14 and then multiplying by 3 to obtain 34 .
  • Write 14 ,  34 on the board and circle it.
• Problem 3: Choose three different students and ask them to share out the cubes/counters so that the different students each get 18 ,  14 and 58 of the total. (Because these fractions have different denominators, this is much more challenging and the students may need more support. Using a representation such as an area model may be needed.) Ask the students what they did and how they knew that they had the right answer? Expect answers such as:
  • ‘We found 18 by dividing 24 by 8 to get 3, then doubled it to get 6, because we know that 28 make up a 14 and 58 was the rest.’
  • ‘We found 18 by dividing 24 by 8 to get 3, then multiplied by 5 so we knew that 58 of 24 = 15 and 18 was the rest’: respond by asking the students how they were sure that the rest of the cubes/counters comprised 58 or 14 of the total.
  • ‘We knew that 14 = 28 from our equivalent fraction knowledge so we first found 18 by finding 24 ÷ 8 =3, so we knew 18 of 24 = 3. We then doubled it to find 28 of 24 = 6 and multiplied by 5 to find 58 of 24 = 15.
  • Write 18 ,  14 and  58 on the board and circle it.
• Problem 4: Split the children into groups of 4 and allocate a set of 24 cubes/counters to each group. Ask the students to share out the cubes/counters so that they receive  112 ,  16 ,  14 and 12 (slide 7). Observe the different groups’ progress and try to identify the two approaches shown below in use and select those two groups to explain how they approached the problem and have students comment of the pros and cons of the different methods. If students do not use the different methods outlined, the teacher may need to highlight these. Two different (but valid) approaches:
  • Using equivalent fractions  112 ,  16   =   212 ,  14   =   312 and  12 =   612 . This is an efficient strategy as the only division then required is to find  112 of 24, for instance that 24 ÷ 12 = 2, and then use multiplication to find the other fractions giving piles of 2, 4, 6  and 12. This method also makes it easy to check that the given fractions comprise the whole and no cubes/counters are left over.
  • Separately finding each fraction by dividing the original 24 cubes/counters, 24 ÷ 12 = 2, 24 ÷ 6 = 4, 24 ÷ 4 = 6, 24 ÷ 2 = 12. This is a more time-consuming method and involves harder steps, that is, more division, which would be more challenging if the number of cubes/counters was a larger and/or less friendly number.
  • Write  112 ,  16 ,  14 and 12 on the board and circle it.
• Ask the students to look at the four circled sets of fractions from Problems 1 to 4 and ask them what they notice about the fractions, what’s the same and different about their numerators and denominators and the whole set. Answers may include:
  • ‘Problems 1 and 2 have the same denominator but the last two sets of fractions have different denominators’: ask students what the impact of this was when sharing out the cubes/counters (made the problem harder and needed an approach of using equivalent fractions with the same denominator).
  • ‘There’s a mix of numerators; in Problems 1 and 4 the fractions all have numerator of 1 (‘unit fractions’), while in 2 and 3 there are other numerators’: ask students what the impact of the non-unit numerators is (first they need to find the unit fraction , for example, 18 , then multiply by say 5 to find 58 ).
  • ‘The problems got harder as we worked down the board’: ask students why this may be the case (mixed denominators, non-unit fractions, less familiar fractions).
  • ‘In each case, the fractions in each set add up to 1’: this is reasonably obvious for Problems 1 and 2 but less so for 3 and 4. It is worthwhile using equivalent fractions to show that in each problem the whole of the cubes/counters are shared out because the fractions all add to 1 whole. This is an important skill needed for the next activity.

Notation note: It is important to be very precise when using notation when finding fractions of an amount. Writing  112 = 12 should be discouraged as this is mathematically false. Ask the students if they would rather that the school holiday lasts for 12 week or 12 weeks to illustrate that these are different numbers. The correct statement is 12 of 24 = 12 or 12 × 24 = 12. 

Creating a class party budget (15 mins)

• Have students work in pairs. Distribute a copy of the Fractional funds budget planning sheet to each pair. These sheets include different expense categories such as decorations, food, drinks, games and prizes. There is an additional line for students to choose another expense category of their own (for example, paper plates/cups, party entertainer, fireworks!).
• Instruct students in their pairs to allocate a fraction of the whole budget to the different expense categories. They need to make sure that their fractions all add to 1 and need to prove it in the space for Question 2. Otherwise, they will spend too much money, or not spend all the budget! Emphasise that their goal is to stay within (that is, spend the whole) budget while ensuring a successful class party.

Differentiation (extension): suggest students pick a range of denominators with harder numbers (for example, twentieths, eighths, ninths, fifteenths) or use percentages.

Differentiation (support): suggest that students pick a range of fractions with the same denominators, for example, all tenths or twelfths. Discourage divisors that are more challenging such as 7 or 13.

• Once students have completed their fractional allocation and proven that the fractions total 1 whole, the teacher can provide them with the total budget, choosing either to set the same budget for the whole class, or differentiating by choosing different amounts for different groups. A good total budget to set is one with many factors such $120, $180 or $240. If students are working in percentages, a multiple of 50 would be recommended, for example, $150, $200 or $250. (Note: if the total budget amount is communicated to students too soon, they may just allocate the dollar-value amount and miss out on the rich fraction exploration in this lesson.)
• Students should then calculate how much they will spend on each category by finding the relevant fraction of the total budget, using the methods explored in the ‘Sharing the whole’ worked examples. They can check their work by adding their dollar amounts and checking that this sum equals the total budget.

Budget pie chart (10 mins)

• Have students create a pie chart to visually represent their budget allocations, by sharing the Fractional funds class party budget Excel file and asking students to type their dollar amounts into the green cells. Students can see how the pie chart automatically calculates the percentage for each category and they should note these on their Budget planning sheet (in the Fraction of total budget column) and compare the percentages with the fractions. Note some of the percentages may be slightly different to expected, which will make for an interesting discussion point (for example, 18 will show up as 13% not 12.5% as the percentages will have been rounded to the nearest whole).
• Alternatively, students can create a pie chart using pen, paper, a pair of compasses and protractors. They will need to multiply the fraction for each expense category by 360° to calculate the correct angle for each sector of the pie chart. This is best done using a calculator or other technologies.

Discussion and sharing (5 mins)

• Encourage a class discussion about the different approaches students took and the trade-offs they made while budgeting.
• Discuss the importance of budgeting, making informed choices, and understanding fractions in practical financial situations.

Summarise the lesson's key points.

• Invite students to reflect on what they've learned.
  • ‘What did you find was the biggest challenge in today’s lesson and how did you overcome it?’
  • ‘Could you explain how to find a set of fractions that add to 1?’
  • ‘How could you find a fraction of an amount, using the example of say 25 of $80?’
  • ‘Do you think the budget you were given was enough and if not, explain why not?’