Year level: Year 5

Strand: Number

Lesson length: 75 min

In this first lesson in the series, students investigate fractions through the relationships between various shapes. They then use tangrams to puzzles to explore fractions. 

This lesson was developed in collaboration with the Australian Association of Mathematics Teachers (AAMT).

Fraction shape puzzles Image

Achievement standard

Students order and represent, add and subtract fractions with the same or related denominators.

Content descriptions

Solve problems involving addition and subtraction of fractions with the same or related denominators, using different strategies. AC9M5N05

Solve problems involving addition and subtraction of fractions using knowledge of equivalent fractions. AC9M6N05

General capabilities

General capabilities

  • Numeracy: Interpreting fractions (Level 7 and Level 8)
  • Critical and Creative Thinking: Generating: Create possibilities
  • Literacy: Speaking and listening

Cross-curriculum priority

Asia and Australia’s engagement with Asia: Understanding Asia’s global significance

  • Reserve time at the end of the lesson for students to reflect and demonstrate their learning.
  • Use the Fraction shape puzzles exit ticket on the teacher's slides (slide 6): ‘If the blue triangle is worth 1, what are the other shapes “worth”? Show your working.’
  • Expect responses such as: Inability to get started; students are unsure of which shape to do next or equivalent fraction shapes.
  • Basic arithmetic skills (addition, subtraction and multiplication).
  • Some background information about numerators, denominators and other basic fractional knowledge, including equivalent fractions.
  • Exposure to tangrams or the relationships between shapes is advantageous.

Some students may:

  • find the introduction of shapes like triangles, squares and parallelograms used as representations of fractions somewhat abstract (particularly for younger students), leading to potential confusion. Refer to real-life examples like 1 2 of a sandwich and 1 4 of an orange to emphasise that they have seen fractions in different shapes before. Encourage students to draw the whole square and divide into halves, quarters etc and compare with the tangram pieces
  • find it challenging to grasp that different visual representations can still represent the same fraction, for example, that different puzzles could both represent 1 2 , even if they look different. Encourage students to replicate equivalent fractions using smaller pieces to confirm that they cover the same area or can be comprised of the same smaller pieces
  • struggle to add fractions with different denominators even using the tangram pieces. Encourage them to subdivide larger pieces and label each part in terms of sixteenths, for example, marking the two halves of the medium triangle and labelling each part  1 16 .

What you need:

  • Lesson plan (Word)

  • Teacher's slides (PowerPoint)

  • Fraction shape puzzles worksheet (Word)

  • Fraction shape puzzles tangram template (Word)

  • Scissors

Preparation tips

  1. Tangram required: one copy (A4) for each students and one teacher copy (A3), pre-cut for demonstration (or physical tangram pieces if available).

Leaning goals

Learning intention

We are learning to find and recognise equivalent fractions, and add and subtract fractions with related denominators.

Success criteria

By the end of this lesson, students can:

  • use tangram pieces to illustrate multiple representations of the same fraction and to represent equivalent fractions, writing equivalent fractions in a number sentence
  • use tangram pieces to create addition and subtraction number sentences for fractions with related denominators.

Why are we learning about this?

In the real world, fractions are used in fields as diverse as construction, retail and cooking. They also have an important role as building blocks for understanding many numerical concepts, including rates and ratios, percentages and, ultimately, advanced algebra and calculus. In this lesson, we will deepen our understanding of fractions using physical manipulatives to gain a deep understanding of equivalence in order to introduce fraction addition and subtraction in an accessible way.

Learning hook 10 mins

Warm-up challenge: Number talk

  • Show students the warm-up image from the teacher's slides (slide 1). Students use mini-whiteboards or their maths book to answer the question: ‘If the image below represents a quarter of the shape, what could the whole shape look like?’
  • Expect responses such as: may cut that shape into quarters; lack of flexibility, for example, will only see it as a fraction one way when there are multiple right answers.
  • Rate the responses: gather or annotate some students’ answers. Have a class discussion as to many of the possible answers.

Differentiation (extension): Create multiple answers using the question ‘what else could it look like?

Differentiation (support): Use concrete materials, peer tutoring.

Explore 50 mins

Explicit teaching (15 mins)

Describe ways to use shapes to communicate fractions.

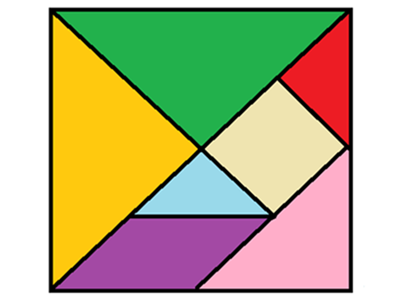
  • Show students the teacher's slides Tangram slide (slide 2), or search for a virtual tangram tool, and discuss its origins as an ancient Chinese puzzle (see Further information).
  • Explain that today we are going to give the whole tangram shape the value of 1 whole, and try to work out the value of all the smaller pieces that make up the whole tangram.
  • Take the A3 pieces and demonstrate how these have been cut from the whole square.
  • Explore the value of each individual Tangram piece using the A3 pieces by finding what fraction of the whole square they each represent. This video (Tangrams 3 part 2) from NSW Department of Education  provides an excellent illustration and discussion of the value of each tangram piece.
  • With student input, explicitly teach the values of the 2 large triangles ( 1 4 ), medium triangle ( 1 8 ), parallelogram ( 1 8 ), square ( 1 8 ) and small triangle (  1 16 ).
  • Key teaching points: all values add to one whole; fractions can look different but still be worth the same value.

Physical practice with tangrams (15 mins)

  • Distribute the Fraction shape puzzles tangram template to each student or pair of students.
  • Have students physically cut out and then re-assemble the tangram pieces to form a square and discuss the total value again.
  • Encourage students to experiment with different combinations and identify the value of individual pieces.
  • As students are working, provide the following focus questions.
    • ‘How does this part connect to the entire shape, and what clues help you understand its relation?’
    • ‘What's the fraction that describes this specific piece?’
    • ‘Explain the connection between these two elements.’
    • ‘Is it possible for two pieces with different shapes to represent the same value?’

‘Can smaller shapes be put together to make bigger pieces?’

Fraction shape puzzles worksheet (20 mins)

  • Refresh students’ understanding of equivalent fractions and introduce fraction addition using slides 3 and 4 in the teacher's slides.
  • Have students complete the Fraction shape puzzles worksheet using their physical tangrams.

Optional: Re-focus student thinking by stating that now they are flexibly working with fractions, they will now work out the various fractions if the large triangle is equivalent to 1 whole, not 1 4 ).

A geometrical puzzle consisting of a square cut into seven pieces which can be arranged to make various other shapes. Pieces include five triangles (two small triangles, one medium triangle, and two large triangles), a square, and a parallelogram. One of the large triangles is shaded.

Summary and reflection 10 mins

Summarise the lesson's key points.

  • Invite students to reflect on what they've learned.
    • Review the worksheet answers as a class, encouraging students to share their findings.
    • Emphasise the connection between tangrams and fractions, highlighting how this knowledge can be applied to addition and subtraction of fractions.
    • Ask the following questions.
      • ‘What aspects of the fraction puzzles intrigued you the most?’
      • ‘What can you share about your understanding of equivalent fractions?’
      • ‘In what creative ways did you apply your knowledge of fractions to craft your own puzzles?’