Year level: 4

Strand: Number / Measurement

Lesson length: 45–60 mins

In this lesson, students learn about place value and how it extends beyond whole numbers. They use drinking straws to model decimals.

Measuring sticks: Decimals Image

Achievement standard

Students use their understanding of place value to represent tenths and hundredths in decimal form and to multiply natural numbers by multiples of 10.

Content descriptions

Students recognise and extend the application of place value to tenths and hundredths and use the conventions of decimal notation to name and represent decimals. AC9M4N01

Students use equivalent representations of fractions using related denominators and make connections between fractions and decimal notation. AC9M4N03

Students interpret unmarked and partial units when measuring and comparing attributes of length, mass, capacity, duration and temperature, using scaled and digital instruments and appropriate units. AC9M4M01

General capabilities

Numeracy

The following formative assessment is suggested for this lesson.

Exit ticket

Choose any item from the classroom and describe its length in units of a whole drinking straw and decimal.

Enabling prompts: What is the length of your chosen item measured using a drinking straw?

Extending prompts: How can you accurately measure the length of your chosen item using a drinking straw?

Assess students on their use of tenths of a straw or whether they more accurately describe length in hundredths of a straw.

Place value: the value of a digit as determined by its position in a number relative to the ones place. For integers, the ones place is occupied by the rightmost digit in the number before the decimal point.

Base-10: a number system which uses the digits 0–9, and the value of the digit is determined by its face value and its place value, for example, 283 = (2 × 100) + (8 ×  10) + (3 × 1) and 283 = 200 + 80 + 3.

Decimal: used to describe aspects of the base-10 number system. The decimal point separates the whole number part of a number from its decimal part.

  • When dividing or multiplying by a multiple of 10, students are often encouraged to ‘hop the dot’ or ‘add a magic zero’. This is unhelpful language for learning. The decimal point never moves and always remains between the ones and tenths. The language of adding a zero confuses students when fractional numbers are involved: for example, 10 x eighteen and a half is not 180.5 or 108.5 it is 185.
  • Students often will apply their whole number thinking when reading and interpreting decimal numbers and will assume that decimal numbers with more digits have a higher value, for example, 0.36 is larger than 0.5, just as 36 is larger than 5 this is known as the longer-is-larger misconception.
  • Students incorrectly read decimals, again applying their whole number thinking, for example, 0.36 is read as zero point thirty-six, instead of stating that we white zero point three six and read it as thirty-six hundredths.

What you need:

  • Lesson plan (Word)

  • Same and different slides (PowerPoint)

  • Place value chart slides (PowerPoint)

  • Drinking straws and scissors

  • Sheet of paper, pencils, markers

Leaning goals

Learning intention

  • We are learning to recognise the extension of the place value system to tenths, hundredths (and thousandths)
  • We are learning to read and recognise decimal notation using strategies and modelling to help us interpret, compare and order decimals
  • We are learning to represent and use decimal notation correctly.

Success criteria

By the end of this lesson, students can:

  • recognise that the place value system can be extended to tenths, hundredths and thousandths
  • read decimals involving tenths, hundredths and thousandths
  • model decimals using materials
  • use models to compare and order decimals
  • use decimal notation to represent decimals
  • develop strategies for reading and interpreting decimals.

Why are we learning about this?

Regrouping numbers into more useful smaller or larger unit sizes occurs in many everyday situations, for example, when working with money (dollars, cents), length (metres, kilometres, millimetres), mass (kilogram, gram) and time (hours, minutes). When using the base-10 system, students use multiplicative thinking to show the relationship between the whole, tenths and hundredths.

Learning hook 5 mins

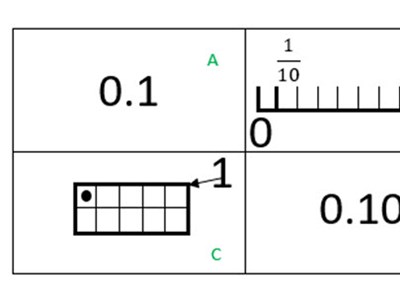
Share the slide, Same and different. Ask students, ‘What is similar? What is different?’

Discussion should centre around the idea that each image represents one-tenth in different ways.

Explore 35–45 mins

Introduce the challenge of finding an object in the classroom that is close in length to three, four or five drinking straws, placed end to end. Explain that they each only have one drinking straw to use as a measuring device. You might want to connect to ancient cultures such as Mayans or Ancient Egyptians that used measuring rods. Discuss ways to ensure accuracy when measuring with their informal measuring device. Provide several minutes to carry out the task.

Ask students to share their findings, explaining how they know if the object is close in length and how they can describe the length using the straw as one unit. Focus on the language they use to describe the part of the straw, such as a small bit/big bit, half the straw, quarter of the straw. Make explicit that when measuring we often need an accurate measurement. Set the challenge of dividing a second straw into 10 equal parts and introduce the term ‘tenths of a straw’. Discuss strategies to ensure the straw is cut into 10 equal parts. Students now re-measure their object and describe its length in units and tenths of a straw. They represent their measured object, using their choice of representation. Make connections between the fraction     1 10   and the decimal notation 0.1.

Explicit teaching

Make explicit how numbers slide in value when divided by 10. Explain that this is the same as multiplying by     1 10  , which we can also say as     1 10   of.

One-tenth of 1000 is 100, one-tenth of 100 is 10, one-tenth of 10 is 1, one-tenth of 1 is … ?

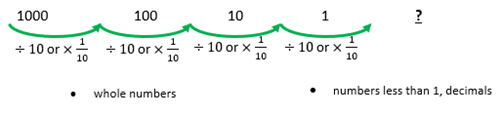
Shows a row of numbers starting from the left: 1000, 100, 10 and 1 Next row shows dividing the top numbers by 10 or multiplying by one tenth has the same effect. This is shown by the green arrows for each number along the top row. 1000, divided by 10 or multiplied by one tenth is 100. 100, divided by 10 or multiplied by one tenth is 10. 10, divided by 10 or multiplied by one tenth is 1.

If needed, remind students that ÷ 2 is the same as finding one-half (×   1 2  ) of a number, for example, 12 ÷ 2 = 6 or   1 2  × 12 = 6 = 12 ×   1 2   , and ÷ 4 is the same as finding one-quarter (×   1 4  ) of a number, for example, 12 ÷ 4 = 3 or    1 4  × 12 = 3 = 12 ×   1 4  , so ÷ 10 is equivalent to ×    1 10  .

CRA model

Display the representations, grouping the objects being measured close in length to three, four or five drinking straws. Ask students which object in each group is closest to the target length and to justify their response. Ask students to order the objects in each group, smallest to largest. Ask them to justify the order.

When students are comparing the lengths of objects, ask when they would choose to label something closer to 3 straws long or closer to 4 straws long – where is the tipping point at which it becomes 4 not 3?

Differentiation

Limited fine motor skills: use a straw graduated into 10 equal parts using a marker instead of cutting into parts or print a line equal in length to the straw with marked in tenths to allow student to still cut the straws (for example, a table 10 x 1, with appropriate column width and no top border).

An empty table 10 x 1, with no top border.

Enabling prompts: How can you add the tenths of a straw?

Extending prompts: What could you do if objects are very close in length? Can you be more accurate than measuring in tenths of a straw?

Summary and reflection 5–10 mins

Pose the problem of needing an even more accurate measurement than one-tenth of the straw. Some students may have measured using the tenth divided into 10 parts. Discuss possible strategies.

Guide discussion towards dividing one-tenth of a straw into a further 10 parts and describe as hundredths.

Ask them next to consider if that were to be cut into a further 10 parts what would we have (thousandths).

Draw a place value chart using a straw as the unit.

Compare to a standard place value chart.

Ask students to reflect on how the use of a straw is similar and different to using a ruler or tape measure.