Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M8A02
Numeracy Progression: Number patterns and algebraic thinking: P7
At this level, students explore linear relationships in the context of the Cartesian plane using digital tools. Students will then go on to find the rule for a linear relationship and solve linear equations, both graphically and algebraically.
Students should be able to identify the variables for a given problem, make a table of values and plot a graph of the values on a Cartesian plane. Discuss with students which is the dependent and independent variable and the meaning, labelling and scale of the axes.
From the line segment drawn, other discussion topics might include the following:
- Can the line be extended beyond the given points?
- What is the meaning of the line?
- What rule could generate the line?
- What is the equation of the line?
When solving equations algebraically, there is a range of techniques students can use. These include:
- the balance method of applying inverse operations
- using a concrete manipulative such as algebra tiles
- using function machines – working forwards and then backwards through an equation or using substitution to verify solutions.
Using contextualised problems helps students to understand the meaning of variables and what an equation represents.
Teaching and learning summary:
- Revise the notion of inverse mathematical relationships.
- Revise algebraic notation.
- Revise and extend knowledge of the Cartesian plane – particularly the labelling and meaning of the axes and the plotting of coordinates.
- Discuss the purpose and meaning of an equation.
- Discuss what makes an equation a linear equation.
- Show how to identify the y-intercept and its meaning.
- Discuss the meaning of the x-coordinate and how to identify its coordinates.
- Show how to calculate the gradient and what it means.
- Demonstrate methods for solving linear equations.
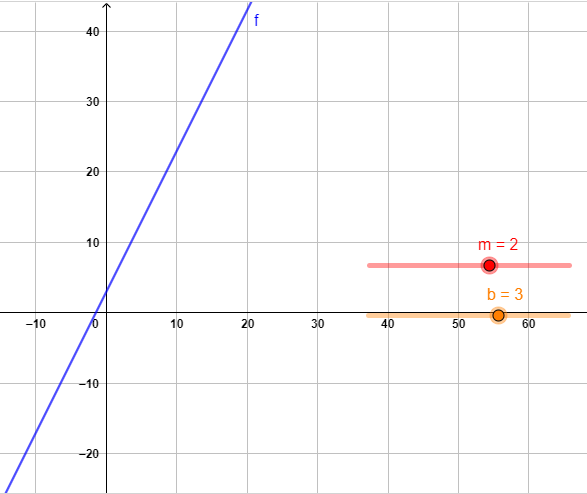
Students will:
- identify an equation as linear
- understand what the variables in an equation represent
- form a table of values from an equation
- draw and label axes accurately
- plot coordinates from a table of values
- find the rule for a linear relationship – identify and calculate the gradient and y-intercept
- solve linear equations using a variety of techniques.
Students may:
- confuse linear graphs and statistical graphs. The notation used may be different for these. This needs to made clear to students and the differences discussed.
- miscomprehend that the gradient can be calculated from any two points along the graph, not necessarily from the origin. Discuss that a line segment has the same properties as a complete line.
- not understand that the linear function does not have to pass through the origin.
- have difficulty with a horizontally flat graph with a 0 gradient. It does not increase in an infinite interval. A vertically straight graph has an infinite gradient. It increases by an infinite amount in an instant.
It is beneficial to create a table of results when plotting a linear function. The coordinate pairs arise from the x and y values.
This resource shows teachers how to identify some of the misconceptions students may hold when solving linear equations and how to address them when teaching.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning how to compare linear relationships by examining their gradients and intercepts.
- We are learning how to solve equations that answer a specific real-world question.
- We are applying our knowledge to make smart decisions and potentially save money on our electricity bill.
Why are we learning about this?
There are so many different options for everything these days. Even picking a soft drink at the shop can be overwhelming. It is important to use mathematical tools to compare our options and make a sensible decision. Linear relationships are very common, and although they might not help us decide which flavoured drink we feel like on a hot day, they can certainly help us to save money.
What to do
Visit the government’s free energy comparison website Energy Made Easy . You might need help from someone at home to enter a few details if you want to be accurate for your own home. Otherwise, select a location and imagine a household of people and their energy usage. This website will then produce a list of different retailers sorted by price. To do this, the website is performing several invisible mathematical operations. Let’s dig into them a little deeper.
Select three plans that you want to compare. Click ‘view plan’ for each and note if there any fees or charges. In the example included here you can see this plan has a total of $58.98 (excluding the credit card payment fee).
- What is the cost per kilowatt/hour (kWh)?
Most retailers offer different rates for different times of the day; this website takes that into account. (You could try that as an extension task too but for now we want to simplify things.) Let’s select a price in the middle. I think 28c/kWh is appropriate here.

Combine your data to form a linear relationship. For this plan we have the following relationship:
Price = $58.98 + $0.28 × kWh
where price is the dependent variable and hours is the independent variable.
Repeat this for multiple plans. Try to find plans that have different offers. Compare plans with low fees and higher hourly rates against plans with higher fees but lower hourly rates. This will be more interesting in the next steps. It might be helpful to fill in a table like this:
| Retailer | Fixed costs | Rate per kWh | Linear relationship |
| Power to the People | $58.98 | $0.28 | p = 0.28k + 58.98 |
| Electrified | $51.13 | $0.31 | p = 0.31k + 51.13 |
Use GeoGebra to graph these relationships.
2. What do you notice about the graphs of the two relationships above?
3. Which has a steeper gradient? Can you predict what we would see if we scrolled to the right?
4. Which of these is a better deal?
5. Is there actually a correct answer to that last question?
6. Based on the comparisons you have made, which plan would be the most suitable to select?
Keep in mind we have over-simplified things a little. You probably need to answer this question in separate parts.
7. Would you suggest a different plan to a single person with a lower energy consumption versus a family with a much larger consumption?
8. At what point does one plan switch from being the more expensive option to being the cheaper option?

To find the exact point at which the plans ‘cross over’, we will need to solve a linear equation. Using the example above, I will put one relationship on the left and one on the right, with an equals sign between. Basically I am asking when these two plans are equal. Pairing that information with the picture above, we can provide the most accurate information.
0.28k + 58.98 = 0.31k + 51.13
7.85 = 0.03k
k ≅ 261.67
Make your final pitch. Present your graphs and equations to a member of your household and have a conversation about which energy retailer might be the best choice. Go back to the Energy Made Easy website and see whether your simplified model makes the same suggestion as the more complex algorithm of the website.
Success criteria
- I can use linear relationships and digital technologies to make informed decisions.
- I can solve equations, create plot graphs and interpret the information provided.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Concrete, Representational, Abstract (CRA)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Worked examples
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource -

Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource -

Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Graphs: formulas and variables
In this lesson, students use algebra and linear equations to model two real-world scenarios.
Go to resource -

Plotting linear relationships
This resource from the AMSI Supporting Australian Mathematics Project gives detailed explanations for teachers and students of the curriculum content, worked examples and assessment questions. It focuses on how to plot points on a Cartesian plane, and how to find the gradient and equation of a line.
Go to resource -

Linear and non-linear relationships
In this resource, teachers are shown how by changing their questions they can guide students to successfully solve problems and understand new concepts. The topics covered include linear and non-linear relationships. There are examples of classroom activities and teacher question stems. The activities are based on the BitL tool.
Go to resource -
Linear relationships on the Cartesian plane
Use this interactive tool and ask students to systematically vary the values of m and b. Ask questions. What do they notice? Can they find any patterns or relationships? Are the relationships linear? What does this mean?
Go to resource
Assessment
By the end of Year 8, students can graph linear relations and solve linear equations with rational solutions and one-variable inequalities, graphically and algebraically.
-

Linear and non-linear relationships
In this resource, teachers are shown how by changing their questions they can guide students to successfully solve problems and understand new concepts. The topics covered include linear and non-linear relationships. There are examples of classroom activities and teacher question stems. The activities are based on the BitL tool.
Go to resource