Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M9A03, AC9M9A04
Numeracy Progression: Number patterns and algebraic thinking: P9
At this level, students work with points, straight lines and line segments on the Cartesian plane, and use the coordinates of points to apply the formulas for calculating the gradient, midpoint and length of a line segment (distance between two points). They use digital tools to represent these points, lines and line segments on the Cartesian plane, explore how these change as the points are varied, and apply them to visually model a range of practical situations and solve related problems.
Students also use digital tools to graph quadratic functions and identify key features of these graphs, such as axis intercepts, symmetry, vertex (turning point) and corresponding maximum or minimum values. They interpret the solutions to quadratic equations graphically, in terms of the points of intersection of horizontal straight lines and parabolas, and determine when the values of a quadratic function lie within a given range. They solve simple equations involving monic quadratics with integer roots algebraically and relate these solutions to the horizontal axis intercepts of the corresponding graph.
Teaching and learning summary:
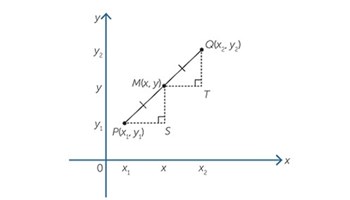
- Have students plot, by hand and with the use of digital tools, various pairs of points across all four quadrants on the Cartesian plane, draw the corresponding line segments, and calculate the gradient, midpoint and length of these line segments.
- Work with students to consider the special cases of a horizontal line segment and a vertical line segment and discuss the meaning of gradient in these two cases.
- Use digital tools to model situations involving shapes in real-life contexts and solve related practical problems, such as the gradient of sections of a bushwalk.
- Have students use digital tools to explore the points of intersection of the graph of a quadratic function with various horizontal straight lines and interpret these with respect to corresponding quadratic equations and their numerical solutions.
- Systematically work through examples with students that show how monic quadratic expressions with integer roots are related to the solution of corresponding quadratic equations and graphs, and have students practise related sets of problems.
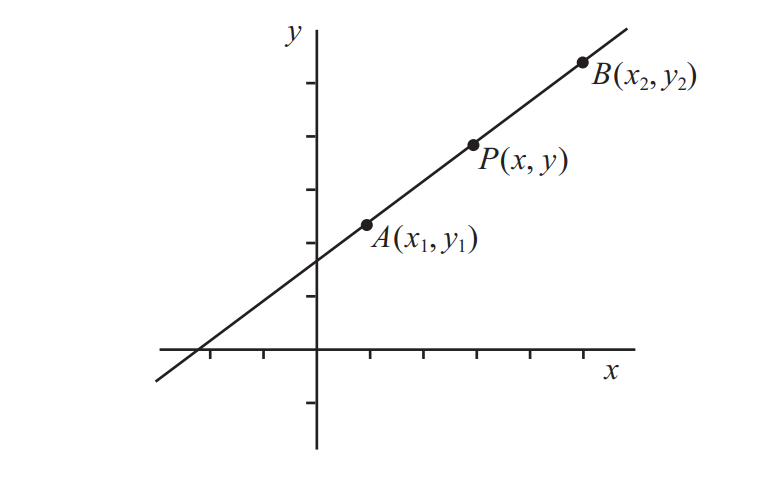
Students:
- find the gradient of a straight line or line segment
- recognise that parallel lines or line segments have the same gradient
- find the coordinates of the midpoint of a line segment given the coordinates of its endpoints
- use Pythagoras’ theorem to find the distance between two distinct points on the Cartesian plane and the length of a line segment between two points
- recognise that quadratic functions have a constant second difference
- identify and graph quadratic functions
- solve monic quadratic equations with integer roots algebraically and graphically, including with the use of digital tools.
Some students may:
- not be clear on the specification and interpretation of coordinates and the positioning of corresponding points in all four quadrants of the Cartesian plane.
- have incorrect memorisation or recall of formulas for gradient, midpoint and distance.
- not be able to interpret and use coordinates correctly in formulas for determining the gradient or the midpoint of a line segment, or not be able to use Pythagoras’ theorem to calculate the distance between two points in the plane.
- not correctly associate a parameter in the rule of a linear or quadratic function with its corresponding graphical property for that type of function.
- not correctly recall the technique for factorising a monic quadratic function and how to apply this to solving a related equation.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- I am learning to find the midpoint between two points on a Cartesian plane.
- I am learning to solve quadratic equations algebraically and graphically.
Why are we learning about this?
Functions and their corresponding graphs are used to describe and help us understand relationships in the world around us. For example, how far a ball thrown up in the air will travel, the steepness of a ski slope, the most suitable shape to use for a bridge,
and so on.
What to do
Find the midpoint between two points
- Plot the two points (–9,4) and (3,4) using a graphing software, such as GeoGebra graphing calculator.
- Now find the midpoint between them
- Plot your point on the same graph to check your answer.
- Repeat the steps above for the two points (2,2) and (2,11).
- Think about the process you used to calculate the midpoints in the steps above. Now see if you can apply this process to find the midpoint between (3, 5) and (14, 19). Plot your point on the same graph to check your answer.
Algebraic and graphical solutions of quadratic equations
- A quadratic function has the rule: y = x2 + x – 7.
Solve this quadratic algebraically for y = 5 and write down your answer(s). - How could you represent the problem in question 1 graphically?
How many graphs would you need to draw?
How are the answers you calculated in question 1 represented on the graphs?
Intersection
The diagram below shows the points of intersection of a horizontal line and the graph of a quadratic function.
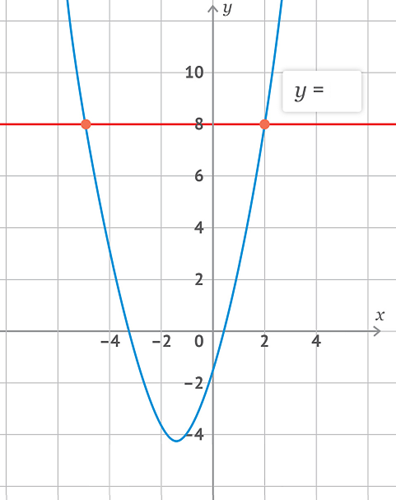
- Write an equation that represents the situation shown on the diagram.
- Use the graph to estimate the answers to this equation.
- Solve this equation algebraically and compare your answers to the estimate.
Success criteria
- I can find the midpoint between two points on a Cartesian plane.
- I can solve quadratic equations algebraically and graphically.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Worked examples
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource -

Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
Introduction to coordinate geometry
This teacher-facing resource provides information on assumed knowledge, topic content, worked examples and exercises for students.
Go to resource -
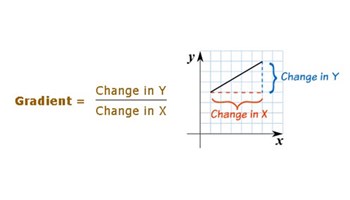
Gradient of a straight line
This interactive and prescriptive tool allows students to calculate the gradient of straight lines with a fixed y-axis intercept, where the corresponding gradient parameter may be altered within the tool.
Go to resource -
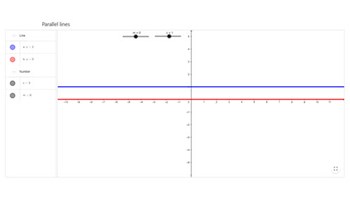
Parallel lines
This interactive tool allows students to vary the parameters that determine the gradient of a pair of parallel straight lines, and the vertical distance between them, to visually investigate the relationship between them.
Go to resource -
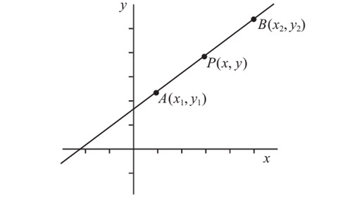
Equations of a straight line
This teacher-facing resource provides a comprehensive overview of linear functions, connecting tables of values, graphs and rules. It includes worked examples, exercises and answers.
Go to resource -
Quadratic equations
This resource provides detailed step-by-step guidance for teachers in the area of quadratic equations, and also includes information on assumed knowledge, motivation, worked examples and the history behind algebra.
Go to resource