Graphs: Year 10: Planning tool

Expected level of development

Australian Curriculum Mathematics V9: AC9M10A03

Numeracy Progression: n/a

At this level, students connect the graphical representation of exponential functions and their corresponding exponential rule. They use digital tools to explore how systematically making changes to the value of the base, pronumerals or variables changes the shape of the corresponding exponential graph.

Students connect repeated multiplication of a number with exponential number patterns and functions, and how this is displayed as a constant multiplier (ratio) between consecutive values of the dependent variable in a table of values. They also develop an appreciation of how the value of the base number affects whether the functions represent growth or decay.

Exponential equations are solved graphically with the use of digital tools and algebraically by applying the index laws. Students are encouraged to revise the exponent laws and expand their application to working with exponential expressions involving negative exponents and simple fractional exponents.

Introduce problems that involve finding the point of intersection between exponential and linear functions.

Teaching and learning summary:

Revise exponent laws with integer values and extend to simple fractional exponents.
Connect the rules of exponential functions with their graphical representations.
Use tables of values to establish if consecutive values of the dependent variable have a constant ratio, and hence represent an exponential function.
Use digital tools to explore the graphs of exponential functions and manipulate variables systematically so that patterns in the changes may be observed.
Solve exponential equations graphically and algebraically using the exponent laws.

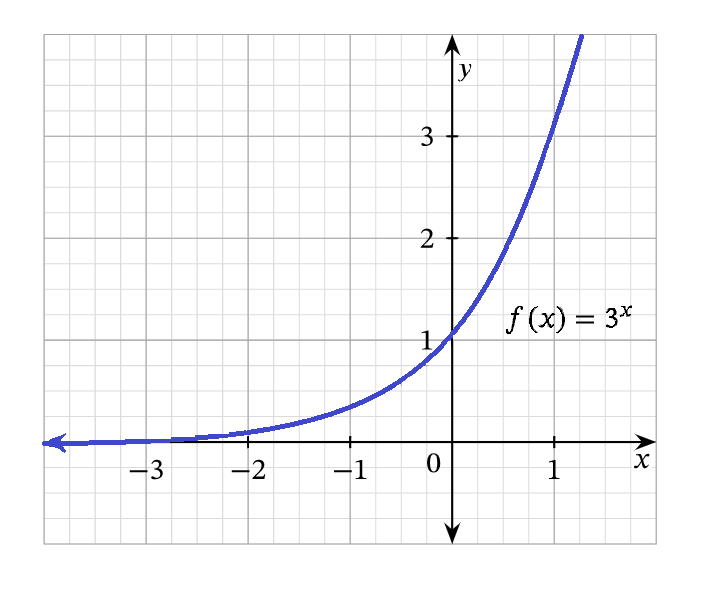
Students will:

connect algebraic and graphical representations of exponential relations
use tables, graphs and algebra to solve exponential equations
use digital tools to explore, investigate and solve problems involving exponential equations.

Some students may:

confuse exponential functions with quadratic functions by having the variable as the base, rather than the exponent. Exponential functions can have different base values; however, the variable is the exponent, for example, 2^x= 16.
underestimate the rapid growth and decay of exponential relations and how this differs from quadratic and linear functions.
misinterpret y = 2 × 3^xas y = (2 × 3 )^x rather than y = 2(3)^x.

The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.

Learning intention

We are learning to connect repeated multiplication of a number with exponential number patterns and functions.
We are learning to identify patterns resulting from varying the base number of the exponential function y = b^x for 0 < b < 10.
We are learning to identify patterns resulting from varying the values of a and c in the rules y = a × 2^x and y = 2^x + c.

Why are we learning about this?

Exponential functions and their corresponding graphs are used to describe and help us understand relationships in the world around us. Some examples are how quickly a virus spreads, depreciation rate of a car, length of time needed to repay a loan, critically evaluating difference alternatives and making predictions about the weather.

What to do

Introductory activities

Start by refreshing and reviewing the concepts of integer exponents and exponential notation here.
Then think about how growth can be represented here.
For each of the following number patterns, decide if it is an increasing (growing) or decreasing (decaying) number pattern. Check your answer by multiplying the next few values in the number pattern using a calculator.

5, 5 × 5, 5 × 5 × 5 …

1.04, 1.04 × 1.04, 1.04 × 1.04 × 1.04 …

0.8, 0.8 × 0.8, 0.8 × 0.8 × 0.8 …

Task 1: Exponential functions with different bases

Use digital tools such as the GeoGebra graphing tool or a graphics calculator to explore the graphs of exponential functions with different base numbers, and observe the resulting patterns.
To start, type y = 2^x into the rule input box on the top left.
Next, type y = b^x into the next rule. Notice the option to add a slider for b, select ‘b’ to add the slider. The graph corresponding to
b = 1 will be shown, which is a horizontal straight line, as 1 raised to any power will be equal to 1, for example: 1³ = 1 × 1 × 1 = 1.
Move slider b to values greater than 1 and compare the resulting graphs to the graph of y = 2^x. Observe any differences and similarities, such as x and y intercepts and changes in the shape of the graph.
Move slider b to values between 0 < b < 1 and compare the resulting graphs to the graph of y = 2^x. Observe any differences and similarities, such as x and y intercepts and changes in the shape of the graph.

Task 2: Exploring more graphs of exponential functions

Use the same tool to explore more graphs of exponential functions.
Enter the following four rules into separate input boxes and observe any differences and similarities. (Note: y = 2 × 2^x can also be written as y = 2(2)^x.)
y = 2(2)^x y = 5(2)^x y = 10(2)^x y = (2)^x2
Now enter the following four rules into separate input boxes and observe any differences and similarities.

y = 2^x + 5 y = 2^x – 8 y = 2^x + 0.5 y = 2^x – 0.9

Success criteria

I can connect repeated multiplication of a number with exponential number patterns and functions.
I can identify patterns resulting from varying the base number of the exponential function y = b^x between 0 < b < 10.
I can identify patterns resulting from varying the values of a and c in the rules y = a × 2^x and y = 2^x + c.

Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.

Planning tool

Year levels

Strands

Topics