Planning tool

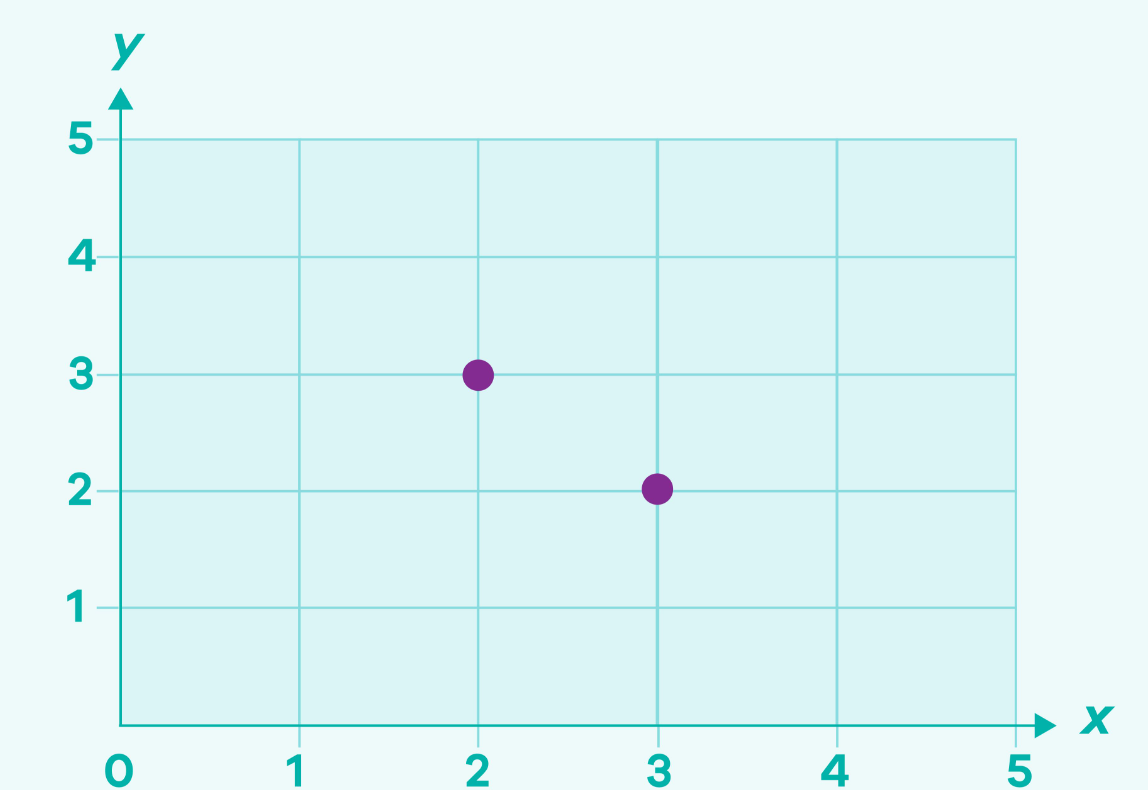
Students will:

• identify and label the elements on a Cartesian plane
• identify a given coordinate pair on a graph
• plot a given coordinate pair on a graph
• correctly write a coordinate pair
• make a table of values from a set of coordinate pairs and identify patterns in the table
• interpret the meaning of a graph of data such as distance/time and temperature/time
• draw a graph that illustrates data, such as distance/time or temperature/time 
• use a digital tool, such as Excel, to record data and plot a graph.

Some students may:

• mix up the x- and y-axes.
• write the coordinates with the y-coordinate first.
• move up/down before right/left.
• label the quadrants clockwise instead of anticlockwise or label the wrong quadrant first.
• not connect the left as negative and the right as positive.
• not recognise that the axes are not located in any quadrant, for example, the point (2, 0) is not located in Q1, it is on the x-axis.
• fail to connect how the coordinates represent real-world data and what that means.

Further notes

Students may have difficulty making the connection between the graph as a picture and the relationships it represents. Using 'storytelling’ to explain what is happening in a graph is a good way for students to make sense of this type of data.

During this topic, begin classes with low-stake activities for students to practise only plotting points and recognising quadrants. For example, generate a set of points that will form a dot-to-dot image when plotted. Include questions such as 'In which quadrant is the image located?'

The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.

Learning intention

• We are learning how to display numerical information on the Cartesian plane.
• We are learning how to analyse a relationship by observing features of a graph.

Why are we learning about this?

Almost anything in our world can be graphed, and these graphical pictures can tell us much more than numbers alone. Are the flood waters rising or falling? How quickly? Is there time to evacuate? When we visualise numerical information, we learn many things about it, such as understanding the past or predicting the future.

What to do

We are going to play a game of ‘guess my code’. To play this game, you will create a secret code by combining any two mathematical operations (+, −, ×, ÷), for example, multiply by 3 and then subtract 4.

Then you will apply the secret code to some of the numbers in the table below, but leave some cells blank.
Remember, order is very important in maths. You might like to see what happens if you apply your code in the opposite order.

This example that uses the sample code mentioned above (multiply by 3 and then subtract 4).

Part A: your turn!

1. Give your partially filled table to another member of your household and see if they can guess the missing numbers and determine your code. If they crack the code, ask them how they did it. What strategies did they use to determine the relationship between the numbers before and after the code? Are there any patterns?
2. Create a new code and fill in a new table. However, this time do not give it to your ‘guesser’; that is, instead, plot your ‘before’ and ‘after’ numbers as points on a Cartesian plane. To explain, using the example above, you would plot the points (–2, –2) in the third quadrant, (0, 4) on the y-axis, and (3, 13) in the first quadrant. Remember that the x-coordinate represents the number before the code was applied and the y-coordinate represents the number after the code is applied.
3. Show your plotted points to your guesser and see if they can determine the points that are missing.
   There should be seven in total, so your x-axis will need to run from –3 to +3.
4. While your guesser is working, notice whether your points are sloping up from left to right or sloping down. Why is this happening? See if you can create a new code with the opposite slope.
5. Now discuss with your guesser whether they found it easier to guess using the table or using the Cartesian plane. Why?
6. Now try playing in reverse. Ask your guesser to create a code for you and see if you can break it with a table or plotted points.

Part B: make connections

Now we are going to try to write your code using mathematical symbols. (Remember those things called ‘variables.’)

1. Let’s call the ‘before code’ number x and the ‘after code’ number y. Using the example above, convert your code to y = x × 3 + 4. Notice how we do not need to put brackets around the x × 3 because multiplication comes before addition in the mathematical order of operations.
2. But we're not quite finished yet. Let’s tidy up the code. We do not need to include the multiplication sign (×) at all, because when we put a number next to a letter, an invisible × is created! So, the code is y= x3 + 4.
3. Wait! That does not look right. One last step. We need to move the 3 in front of the x. This makes sure we are following the convention that mathematicians have used for hundreds of years. We should not spoil that tradition. So finally, y = 3x + 4.
4. Can you convert all your codes into mathematical symbols (equations)? Try to spot a specific pattern.
5. Study the tables you created and notice by how much the ‘after code’ values are increasing or decreasing with each step.
6. Is there any link between this increase/decrease and a particular spot in your newly formed equations?

Success criteria

• I can create a set of ordered pairs with a linear relationship.
• I can plot these pairs on the Cartesian plane.
• I can determine whether my relationship is increasing or decreasing and compare how steep it is.