Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M4N09
Numeracy Progression: Number patterns and algebraic thinking: P4
At this level, students create and follow algorithms involving a sequence of steps and decisions to generate number patterns involving addition or multiplication. They analyse the patterns generated and describe and explain them.
Students use digital tools such as spreadsheets and calculators to model and follow algorithms, and to enable them to explore algorithms using larger sets of numbers.
The algorithms can be based on a variety of activities such as generating number sequences involving multiples of one to 10 or multiplying/adding by a constant term. Students also create their own algorithms as a set of instructions, using flowcharts and lists, and share them with classmates to follow.
Teaching and learning summary:
- Create and follow algorithms involving a sequence of steps and decisions that use addition or multiplication to generate number patterns.
- Work with algorithms involving activities such as generating number sequences involving multiples of one to 10 or multiplying/adding by a constant term. For example, use a spreadsheet to add or multiply by 10 to each number from 0 to 200.
- Use digital tools such as spreadsheets and calculators to model and explore algorithms with larger sets of numbers.
- Analyse patterns generated and describe and explain them.
- Use flowcharts or lists to create algorithms as a set of instructions that classmates can follow.
Students:
- follow algorithms involving a sequence of steps and decisions to generate number patterns using addition or multiplication
- use digital tools such as spreadsheets and calculators to model and explore algorithms
- identify, describe and explain emerging patterns in the number patterns generated
- use flowcharts or lists to create an algorithm as a set of instructions that a classmate can follow.
Some students may:
- not understand that an algorithm is an ordered set of instructions
- not realise that each step must be explicitly included in an algorithm
- have difficulty describing steps and actions using written instructions with words and mathematical expressions.
To support and build understanding, provide opportunities to explore algorithms in different formats such as a list of steps or as a flowchart. As students follow an algorithm, they will begin to understand their use and see how they are helpful.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning to generate a sequence of numbers using a spreadsheet.
- We are learning to analyse and describe the number sequence ‘multiplying by 11’.
- We are learning to use our findings to predict the next 10 numbers in the given sequence.
Why are we learning about this?
Algorithms are a set of steps or rules to follow to help complete a task. The process for adding 3-digit numbers, for example 345 + 259, is an example of an algorithm. Computer programmers write algorithms that instruct computers how to complete a task.
What to do
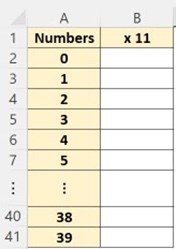
1. Using a spreadsheet, create a table that has two columns like the one shown below. Fill the left column with the numbers 0 to 39.
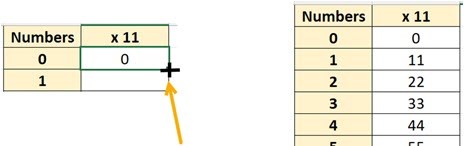
In cell B2, enter the formula ‘=A2*11’ and press ENTER. You should now see the number 0 in B2.

2. Use the ‘fill down’ function to generate a sequence for ‘multiply by 11’ from 0 to 39. (Hint: Move your cursor to the bottom right of cell B2, until you see a solid cross, hold the mouse down and drag your cursor all the way down to 39.)
3. Analyse the sequence generated from input numbers 0 to 9. Describe any pattern you notice. Can you explain why this pattern is generated when multiplying by 11?
4. Now analyse these two sections of the sequence: 10 to 19 and 20 to 29. Describe how the patterns in these two sections are similar and how they are different from each other.
5. Look at the section from 30 to 39. Is this pattern similar to the one you described in part c?
6. Use your findings from parts c and d to predict what you think the sequence will be from 40 to 49. Write it down on a piece of paper.
7. Check your results from part e by extending your table to 49 in the left column and extending the sequence in the right column.
Success criteria:
I can:
- generate a number sequence using a spreadsheet
- analyse and describe the number sequence ‘multiplying by 11’
- use my findings to predict the next 10 numbers in the given sequence.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Concrete, Representational, Abstract (CRA model)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Collaborative learning
For group work to be effective students need to be taught explicitly how to work together in different settings, such as pairs or larger groups, and they need to practise these skills.
Go to resource -

Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
Developing flowcharts: Halving strategy
In this lesson, students create a flowchart outlining the sequence of steps required when using the halving strategy for division.
Go to resource -
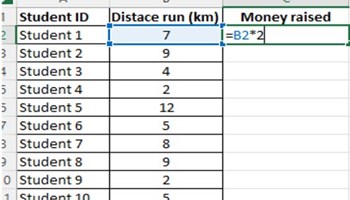
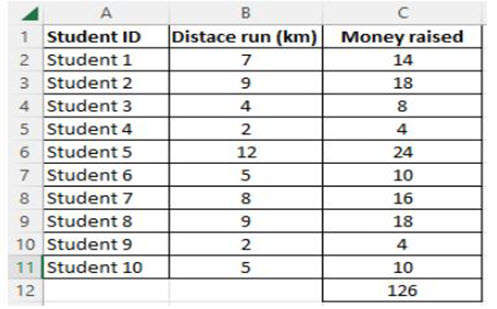
Sponsored fun run
In this lesson, students generate a sequence of numbers using a spreadsheet. This is an example of a simple algorithm ‘multiplying by a number’.
Go to resource -
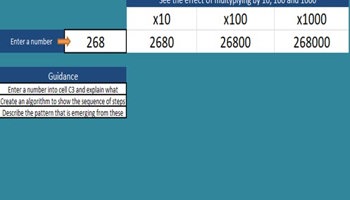
Multiply by 10, 100, 1000
Use this spreadsheet to show students how to automate the multiplication of a number by 10, 100 and 1,000.
Go to resource -

Number Pattern explorations
This activity discusses how number patterns can be created, and how to note properties and emerging patterns in these.
Go to resource
