Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M3N07
Numeracy Progression: Number patterns and algebraic thinking: P3
At this level, students create and follow algorithms involving a short sequence of steps to generate number patterns. They use digital tools such as spreadsheets and calculators to explore algorithms with larger sets of numbers. Students identify any patterns generated and describe and explain them.
The algorithms can be based on a variety of activities such as doubling, halving and exploring multiples. Students can also create their own algorithms as a set of instructions that a classmate can follow. Support students to be explicit with each instruction and to note when ‘errors’ occur.
Support students to follow and create algorithms of varied representations including, flowcharts, commands, instructions and equations to develop a broad understanding of their application in mathematics.
Teaching and learning summary:
- Collaboratively create and follow algorithms involving a sequence of steps to generate number patterns.
- Work with algorithms involving activities such as doubling, halving and multiples, for example, determining whether a given number is a multiple of 2, 5 or 10.
- Use digital tools such as spreadsheets and calculators to explore algorithms with larger sets of numbers.
- Analyse patterns generated and describe and explain them.
- Create an algorithm as a set of instructions that a classmate can follow. For example, generate multiples of 3 using the rule ‘to multiply by 3 you double the number and add on one more of the number’.

Students will be able to:
- follow algorithms involving a sequence of steps to generate number patterns
- use digital tools such as spreadsheets and calculators to explore algorithms
- identify, describe and explain emerging patterns in the number patterns generated
- create an algorithm as a set of instructions that a classmate can follow.
Some students may:
- not understand that an algorithm is an ordered set of instructions
- not recognise that each step must be explicitly included in an algorithm
- be able to follow an algorithm but have difficulty describing steps and actions using written instructions with words and mathematical expressions.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning to recognise when a number is a multiple of 2, 5 or 10.
- We are learning that when multiplying an odd number by 5 the resulting number is odd.
- We are learning that when multiplying an even number by 5 the resulting number is even.
Why are we learning about this?
Algorithms are a set of steps or rules to follow to help complete a task. Following a recipe to bake a cake or following the rules of a board game are examples of how we apply algorithms in everyday life.
What to do
Create a table that has a row of the numbers from 1 to 20 across the top and a column of the numbers 2, 5 and 10 down the left.

1. Complete the first row in the table by multiplying each of the numbers across the top by 2 and placing the result into the table.
- Describe any patterns you notice and explain them.
- Look at the last (units) digit for each result (for instance, for 36 this is 6). List all the different last digits that you can see and comment on anything you notice.
2. Complete the second row by multiplying each of the numbers across the top by 5 and placing the result into the table.
- Describe any patterns you notice and explain them.
- Look at the last (units) digit for each result (for instance, for 25 this is 5). List all the different last digits that you can see and comment on anything you notice.
3. Complete the third row by multiplying each of the numbers across the top by 10 and placing the result into the table.
- Describe any patterns you notice and explain them.
- Look at the last (units) digit for each result (for instance, for 130 this is 0). List all the different last digits that you can see and comment on anything you notice.
4. Use your findings from questions 1, 2 and 3 to help answer these questions. For each of the numbers below, decide if they are a multiple of 2, 5 or 10. Remember, a number can be a multiple of more than one other number.
35
88
160
754
895
5. Look at your table and identify the results that are odd numbers. Colour in the squares with odd number results.
- What do you notice?
- Is the result odd when an even number is multiplied by 5 or when an odd number is multiplied by 5?
Success criteria
I can:
- recognise when a number is a multiple of 2, 5 or 10
- understand that when multiplying an odd number by 5 the resulting number is odd
- understand that when multiplying an even number by 5 the resulting number is even.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Concrete, Representational, Abstract (CRA model)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Collaborative learning
For group work to be effective students need to be taught explicitly how to work together in different settings, such as pairs or larger groups, and they need to practise these skills.
Go to resource -

Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
Year 3: Number code investigation
In this lesson, students explore the idea of functions and inverse functions to decode simple algorithms.
Go to resource -

Year 3: Number paths
In this lesson, students use their understanding of directional language to investigate number paths through a number grid. They use basic addition facts to complete the task.
Go to resource -

reSolve: Multiplication: Domino Arrays
This is a useful precursor activity involving systematic reasoning with rectangular arrays to model multiplication and factors.
Go to resource -
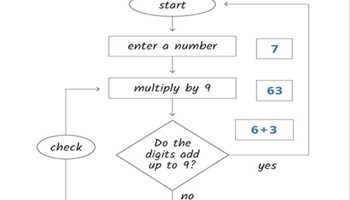
Algorithms: Multiplying by 9
In this task, students follow an algorithm to observe number patterns in the 9 times tables and multiples of 9.
Go to resource
