Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M4A01
Numeracy Progression: Additive strategies: P8, Number patterns and algebraic thinking: P4
At this level, students further develop their algebraic thinking and strategies to find missing or unknown numbers in addition and subtraction related problems.
Use relatable contexts for problems that require students to represent the unknown number using an appropriate equation. Use questioning strategies to prompt students to communicate their reasoning when working out the unknown value in an equation. Draw out their thinking about the connections between addition and subtraction. Share examples of strategies students use in order to build their range of strategies for computation.
Make explicit the importance of equivalence when solving number sentences. A useful approach is to use true/false statements to investigate if both sides of an equation are equal. For example, present the equation 26 – 19 = 15 – 8. Use a number talk to use different strategies to solve the problem. Build on students’ strategies and piggyback off their explanations to make learning explicit. Use models such as part-part-whole diagrams or bar models to partition numbers. Use a number line to show whether both sides of an equation are equivalent. Look for opportunities to demonstrate the use of commutative properties of addition, for example,
7 + 6 = 6 + 7.
Use maths games that draw on additive thinking and use of number facts, including strategy games, to reach a target number or balance beams to balance equations.
Teaching and learning summary:
- Demonstrate the commutative properties of addition using materials, diagrams and number lines.
- Use balance scales and informal uniform units to create addition or subtraction number sensors showing equivalence.
- Use relational thinking and knowledge of equivalent number sentences to explain whether equations involving addition or subtraction are true.
- Use part-part-whole diagrams or bar models to recognise and explain the inverse relationship between addition and subtraction, using this to make calculations easier.
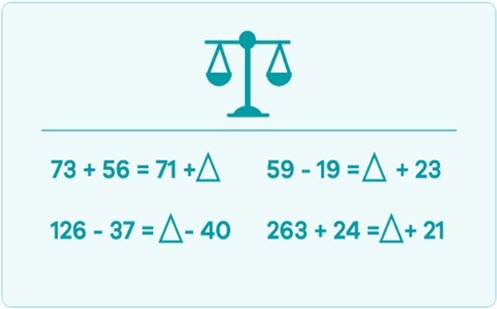
Students:
- partition numbers including two-digit numbers as a composition of other numbers
- use models to solve addition and subtraction problems involving two-digit numbers
- interpret number problems to identify known and unknown parts
- recognise and explain the relationship between addition and subtraction using materials and representations.
Some students may:
- not yet understand the meaning of the equals sign. Often students will think that the equal sign means ‘the answer is’, while the equal sign in fact means ‘the same as’ or ‘equivalent to’. Although students may understand the idea of equivalence, some may solve the problems using a computational approach. For example, if students are presented with the equation 26 + 39 = ? + 23, they might first calculate the left-hand side to get 65, and then reason that they need to find the number that is added to 23 to get 65. This is a computational approach. Support these students to see the relationships between number expressions by helping them focus on the properties of the operation of addition that is critical for algebra. For example, point out to students that 26 is 3 more than 23, therefore the missing number must be 3 more than 39, making it 42.
Refer to the article Getting the balance right to discover common misconceptions surrounding the equals sign, and ways to help learners develop their understanding.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning to complete simple number sentences by calculating the missing value.
- We are using our addition and subtraction knowledge to balance out equations with a missing number.
Why are we learning about this?
- An important area of maths learning is about finding missing or 'unknown' values.
What to do
1. Look at this maths problem. What do you know from the information given?
2. Write down some facts that can be used to solve the problem:
- What is the mass of each ball?
3. To get you started, what do you notice about the mass of the football and the soccer ball?

4. Explain how you worked this out.
Success criteria
I can:
- use addition and subtraction to calculate unknown values
- use appropriate terminology to describe mathematical ideas.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Concrete, Representational, Abstract (CRA)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Number Talks
An illustration of a teacher running a number talk with a lower primary class
Go to resource -
Multiple exposures
Providing students with multiple opportunities within different contexts to practise skills and apply concepts allows them to consolidate and deepen their understanding.
Go to resource -

Using games and storybooks
Games and storybooks are great resources to use in the classroom and are engaging for students.
Go to resource -

Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource -
Feedback
It has been shown that good feedback can make a significant difference to a student’s future performance.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
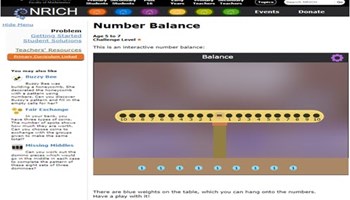
Number balance
Students use their knowledge of number bonds to develop their algebraic reasoning skills.
Go to resource -

Which symbol?
This problem requires children to utilise their knowledge of number bonds in an unusual context, and offers the opportunity for them to explain and reason through their solutions.
Go to resource -
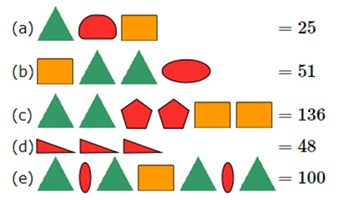
Super shapes
This problem provides an opportunity for pupils to practise using addition and subtraction, and reinforces their inverse relationship.
Go to resource -

reSolve: Algebra: Chess – The King
This lesson aims to build students' algebraic reasoning and understanding of number as they explore computation on a number chart.
Go to resource -
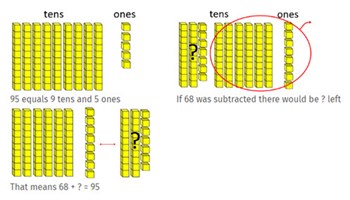
Addition and subtraction with whole numbers
This unit explores situations that involve addition and subtraction of whole numbers. Students are expected to choose among a range of strategies, based on their understanding of place value.
Go to resource -
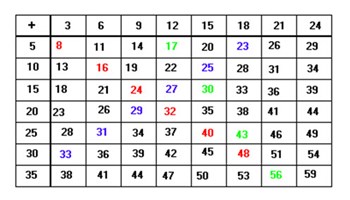
Sara's table
This problem provides students with the opportunity to look for patterns in addition.
Go to resource -

Number relations
This unit of work investigates how relational thinking is applied to number operations.
Go to resource
Assessment
At the end of Year 4, students find unknown values in numerical equations involving addition and subtraction.
-

Assessment: True or false?
Use the task True or false to determine students understanding of equivalence. This can be used as formative assessment.
Go to resource -

Assessment: Balance equations
Use the task Balance equations to determine students’ understanding of equivalence. This can be used as formative assessment.
Go to resource