Year level: 4

Strand: Number

Lesson length: 60 mins

In this lesson, students learn about place value and how it extends beyond whole numbers. They use decimal notation to name and represent decimals and use materials to model decimals. These models help students to order and compare decimals that include tenths, hundredths and thousandths.

After completing the lesson, a relevant follow-up activity is Decimats (understanding fractions).

Recognising and comparing decimal numbers Image

Achievement standard

By the end of Year 4, students use their understanding of place value to recognise, represent and compare tenths, hundredths and thousandths in decimal form.

Content descriptions

Students recognise and extend the application of place value to tenths and hundredths and use the conventions of decimal notation to name and represent decimals. AC9M4N01

General capabilities

Numeracy

  • Provide the exit ticket, which enables students to choose and compare two decimal numbers from a table.
  • Assess students’ proficiency in naming numbers and accurately comparing the numbers identifying the larger number.
  • Observe if they can accurately record the number using a place value chart.

Some students may:

  • apply their whole number thinking when reading and interpreting decimal numbers and will assume that decimal numbers with more digits have a higher value, for example, 0.36 is larger than 0.5, just as 36 is larger than 5; this is known as the ‘longer is larger’ misconception. Using materials, such as decimats, can help students to model and compare decimals and overcome this common misconception.
  • incorrectly interpret a decimal fraction, for example, 2.75 should be read as ‘two and seventy-five hundredths’. Reading it as ‘two point seven five’ can lead to confusion and a misunderstanding of the decimal's value. Using place value helps reinforce the understanding of the relative sizes of the digits and their positions in the decimal number. Understanding place value is crucial when working with decimal fractions.

Prior to this lesson, it is assumed that students have knowledge of:

  • Place value: the value of a digit as determined by its position in a number relative to the ones place. For integers, the ones place is occupied by the right-most digit in the number before the decimal point.
  • Base 10: a number system which uses the digits 0–9, and the value of the digit is determined by its face value and its place value, for example, 283 = 2 × 100 + 8 × 10 + 3 × 1 and 283 = 200 + 80 + 3.
  • Decimal: used to describe aspects of the base 10 number system. The decimal point separates the whole number part of a number from its decimal part.

What you need:

Learning goals

Learning intention

We are learning to:

  • recognise the extension of the place value system to tenths, hundredths and thousandths
  • read and recognise decimal notation using strategies and modelling to help us interpret, compare and order decimals
  • represent and use decimal notation correctly.

Success criteria

By the end of this lesson, students can:

  • recognise that the place value system can be extended to tenths, hundredths and thousandths
  • read decimals involving tenths, hundredths and thousandths
  • model decimals using materials
  • use models to compare and order decimals
  • use decimal notation to represent decimals
  • develop strategies for reading and interpreting decimals.

Why are we learning about this?

We use decimals in everyday situations, including when measuring length and reading digital scales. This lesson will help students interpret decimals by introducing them to the use of decimats, which are graphic organisers that enable students to model tenths, hundredths and thousandths.

Learning hook 10 mins

  • In this part of the lesson, use a number line to support students to understand and apply place value when working with decimal fractions.
  • Ask students where they might use decimal numbers in daily life? List their ideas.
  • Use the Decimal fractions video to explore decimal numbers, and how they are used and represented in everyday contexts. You can use the video to develop the language of tenths to describe one whole divided into 10 equal parts and hundredths to describe to one-tenth divided into 10 equal parts.
  • Model how to write a decimal number including tenths and hundredths on a number line. Use the number line to compare two decimal numbers.
  • Note: The accompanying teaching guide for the decimal fractions video provides suggested ways to follow up the video, which can be followed up in future lessons.

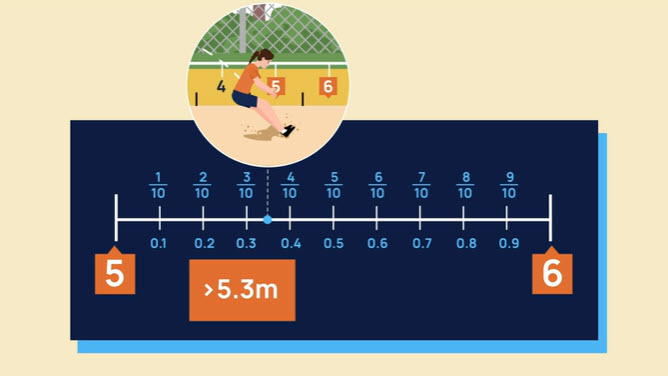
A number line showing tenths

Image from video: Decimal fractions showing a number line

Explore 40 mins

Download the teacher’s slides to accompany your teaching.

Explicit teaching (20 mins)

  • Write two decimal numbers on a whiteboard and ask students to name the decimal numbers and which is larger. An example might be 0.4 and 0.26. Students with the ‘longer is larger’ misconception will likely say 0.26 is larger than 0.4.
  • Use the teacher’s slides (slide 2) to display a place value chart. Model reading each decimal number using place value language, for example, 0.4 is read as four-tenths and 0.26 is read as twenty-six hundredths.
  • Explain to students that we can also use a place value chart to help us recognise which decimal is larger. For example, for the first pair of decimals 0.4 is four-tenths, whereas the second decimal 0.26 has only two-tenths, so the first decimal is larger. Compare other decimals including those that include thousandths.

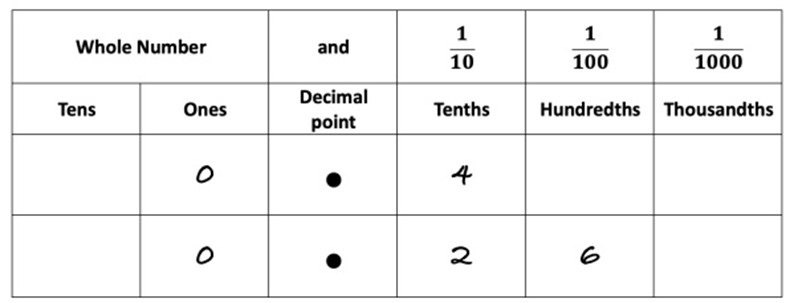
A place value chart

Image: Place value chart

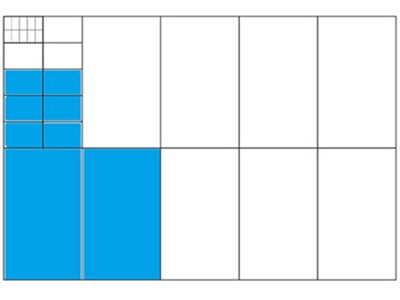
  • Explain to students that another way to name and compare decimal numbers is to use a visual model called a decimat. Explain that decimats can also be used to model decimal numbers using place value.
  • To help students understand how to use a decimat, use teacher modelling to show how one whole can be divided into tenths. Next show how tenths can be divided into 10 equal parts to make hundredths, and then show how hundredths can be divided into 10 equal parts to make thousandths. Explain that this is linked to the base-10 number system. Show shaded models of these numbers (slides 3–8). Note: clicking the mouse advances animations to reveal shaded grid parts (refer to the notes provided on each slide).
  • Introduce a decimat and numbers represented by shading parts of the decimat. Use teacher modelling to use place value to name the decimal number represented by the shaded area of the decimat (slides 9–11).

Practical component (20 mins)

  • Provide each pair of students with the Using a decimat worksheet.
  • First, have students work together in pairs to name the decimal number represented by the shaded decimats.
  • have students choose their own numbers to represent using the blank decimats provided.

Differentiation

  • Support: Work only in tenths. Can you give me an example of a number that includes tenths?
  • Enabling: How can you compare two decimal numbers? Which is larger?
  • Extending: Can you give me an example of a way we use thousandths in real life?

Summary and reflection 10 mins

Display two decimal numbers. Ask students to compare the two decimal numbers and explain which model they would choose to represent the numbers: a place value chart, a number line or a decimat model? Which visual aid do they prefer and why?