Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M9M01
Numeracy Progression: Understanding units of measurement: P9
At this level, students will calculate the surface area, volume and capacity of cylinders and solve related problems.
Using nets, students will see that the shapes that make up the surface area of a cylinder are two circles and a rectangle. They should know that the rule for the surface area of a cylinder is: A = 2πrh + 2πr2.
Building on students’ previous knowledge of the volume of prisms (Volume = Base Area × Height, where the base area is the same cross-sectional area throughout the height), the formula for the volume of a cylinder can be derived. Students will see that the base area is πr2 and therefore the rule for the volume of a cylinder will be V = πr2h.
The use of concrete materials, such as play dough, can help students to visualise the cross-section of different objects, such as a cylinder. The use of nets demonstrates that area is a 'flat' or two-dimensional (2D) quantity and so to find surface area students need to find the area of each surface of the shape. Turning the nets into a 3D solid will show students that volume is the amount of space occupied by an object.
Identifying, understanding and using the correct units of measurement for volume and area allows students to communicate with specificity and context. Students consolidate their understanding of using and providing units to show that their calculations, formulas and comparisons are correct for different contexts.
Teaching and learning summary:
- Revise knowledge of circles, such as circumference and area.
- Connect knowledge of circles and nets to find the surface area of a cylinder.
- Connect knowledge of the volume of a prism to finding the volume of a cylinder.
- Expand knowledge of the connection between volume and capacity.
- Use knowledge of circles and cylinders to solve problems.
- Connect knowledge of circles and cylinders with knowledge of other shapes and objects to find the area, surface area and volume of composite shapes and objects.
- Provide opportunities for students to use these rules in solving surface area and volume-related problems.
- Ensure students identify, understand and use correct units of measurement for volume and area.
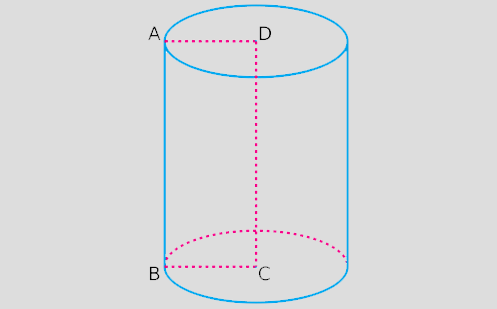
Students:
- draw the net of a cylinder
- calculate the surface area of a cylinder from a net
- calculate the volume of a cylinder
- solve simple problems involving the surface area and volume of a cylinder
- combine knowledge of circles and cylinders with knowledge of other shapes and objects to find the area, surface area and volume of composite shapes and objects.
Some students may:
- confuse radius and diameter.
- not appreciate that π is a number.
- use the wrong measurement.
- have difficulty in leaving answers in terms of π, preferring rounded decimals.
- have difficulty in visualising the net of a cylinder.
- confuse the various formulas for the area of a circle and the volume of a cylinder.
- confuse the rules for surface area and volume.
- be confused by the word ‘base’. They should be able to recognise this does not always refer to the ‘bottom’ of the object, but the face by which the prism or pyramid is named.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are expanding knowledge of circles to three-dimensional objects such as cylinders.
- We are learning how to calculate the surface area and volume of a cylinder.
- We are learning how to apply our knowledge of circles and cylinders to practical situations.
Why are we learning about this?
A knowledge of area and volume is useful in many situations, such as wrapping presents and filling containers.
What to do
Total surface area and volume of a cylinder
- Open this GeoGebra exercise: Total surface area and volume of cylinder (with net shown).
- Follow the activity prompts that will lead you through finding the surface area and volume of a cylinder.
- Use the interactive net to vary the radius and height of the cylinder. Create at least three cylinders of different sizes.
- Draw or take a screen capture of your results.
Finding the volume and surface area of a cylinder
- Open the resource Efficient cutting. Using a sheet of A4 paper, your challenge is to find those dimensions that allow you to make a cylinder with the greatest volume.
- Work through the task, creating a cylinder with these dimensions. Next, work out the surface area of your cylinder.
- Explain how you worked it out.
Success criteria
- I can draw the net of a cylinder.
- I can calculate the surface area of a cylinder from a net.
- I can calculate the volume of a cylinder.
- I can solve simple problems involving the surface area and volume of a cylinder.
- I can combine my knowledge of circles and cylinders with my knowledge of other shapes and objects to find the area, surface area and volume of composite shapes and objects.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Concrete, Representational, Abstract (CRA)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
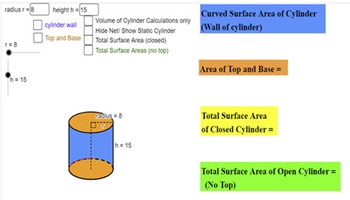
Surface area and volume of a cylinder
This resource gives a dynamic visual representation of the net of a cylinder and shows the various associated formulas for surface area and volume.
Go to resource -
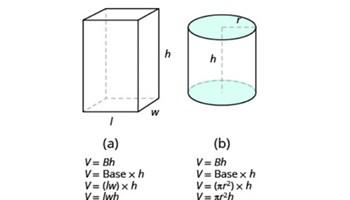
Finding the volume and surface area of a cylinder
This resource describes how the formulas for the surface area and volume of a cylinder are derived. It shows a worked example and sets two problems for students to work through.
Go to resource -
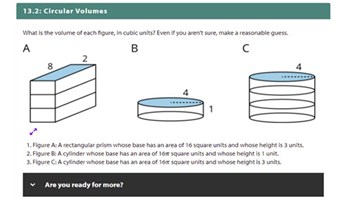
The volume of a cylinder
Calculate the volume of a cylinder and compare and contrast the formula for the volume of a cylinder with the formula for the volume of a prism.
Go to resource -
Finding cylinder dimensions
These tasks build on students’ knowledge of prisms and circles to develop their understanding and ability to solve problems involving the volume of a cylinder.
Go to resource -

Mathematical modelling: packaging designer
A series of five units that investigates cylindrical objects such as candles and bottles, and applies mathematical-modelling processes.
Go to resource
