Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M10M01
Numeracy Progression: Understanding geometric properties: P7
At this level, students will extend their application of volume and surface area to solve problems on composite solids. Students will need to be able to visualise the individual elements of the composite solids and identify the areas where these elements touch.
This topic has connection with ratio and proportion, circles and cylinders, and Pythagoras and trigonometry.
Students are required to identify and use the correct units appropriate to a particular problem.
Teaching and learning summary:
- Build on students’ understanding of area and volume.
- Introduce surface area.
- Introduce the formula for the volume of a prism – cross-sectional area × height.
- Make connections to composite area.
- Make connections to circles, cylinders and cones.
- Use appropriate units pertaining to surface area and volume.
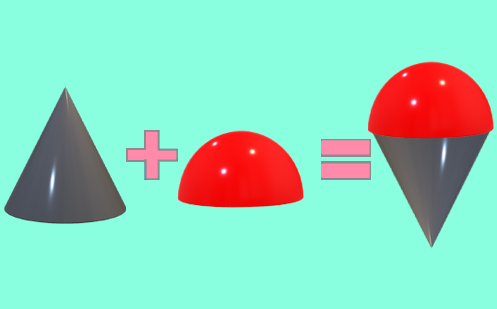
Students:
- can identify prisms
- use the formula to find the volume of a prism
- use the correct units for volume
- use their knowledge to solve problems involving prisms and cylinders and composite objects
- can use appropriate units pertaining to surface area and volume.
Some students may:
- confuse area and volume.
- give the solution with incorrect units
- find the product of all measurements given, not just those that they need.
- believe that for all prisms you multiply three dimensions, not appreciating it is the cross-sectional area × length.
- get confused with the terminology length, height and width when shown the same object in different orientations.
- be unable to visualise the unobserved sides of a solid object.
- not split the solids correctly.
- be unable to visualise the shared sides of a composite object, and so do not calculate the surface area correctly.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning to calculate the volume and surface area of composite solids.
Why are we learning about this?
There are many occasions when you need to know the volume or surface area of an object – from wrapping a present to calculating how much paint you will need to paint a wall.
What to do
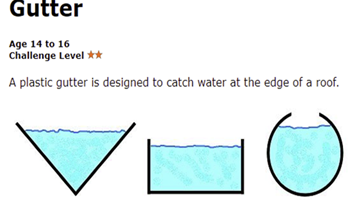
Volume of a water tank
In this activity you will be calculating the volume of water in different sized tanks. There are a couple of limitations: the base of the tank must fit into an area of 3 m2, and the tank must hold 20,000 L.
- Complete the table in Activity 3.
Designing a fish tank
You would like to make a tank for your pet spider, Eric. You have 1 m2 of clear plastic to work with.
- Assuming you can use all the plastic, with no wastage, what shaped tank will have the greatest volume (the most space for Eric to move about)?
- You do not want Eric to escape, so the tank is a closed box. Calculate the dimensions of the tank, so that the surface area is no more than 1 m2.
- Calculate the volume of the tank.
Here are some ideas for tank shapes to get you started:
- cube
- cuboid
- hexagonal-based prism
- cylinder
- pyramid
- cone
- sphere.
Success criteria
- I can identify different prisms
- I use the formula to calculate the volume of a prism
- I can identify the shapes of the base/top of a prism
- I can calculate the surface area of a prism
- I can visualise the different elements in a composite solid
- I can calculate the volume and surface area of a composite solid
- I use the correct units of measurement for volume and area.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Concrete, Representational, Abstract (CRA)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

A piece of cake
In this lesson, students build on their skills in finding volumes and surface areas of prisms and cylinders to design a multi-level celebration cake for a party.
Go to resource -
Solid geometry
In this unit, students practise spatial visualisation in three dimensions, and study the effect of dilation on area and volume.
Go to resource -
Volume of a pyramid and a cone
A proof of the formula for the volume of a pyramid and a cone using the ancient Chinese yangma.
Go to resource