Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M9M03
Numeracy Progression: Understanding geometric properties: P7, Understanding units of measurement: P10, Proportional thinking: P7
At this level, students apply and build on knowledge of Pythagoras’ theorem, angle properties, trigonometry and scales to solve problems involving right-angled triangles.
Students will use a variety of authentic contexts to find distances between points on a Cartesian plane. They use knowledge of similarity and ratios to find the lengths of the sides of triangles. Students solve practical problems using Pythagoras’ theorem and communicate their thinking, reasoning and solutions.
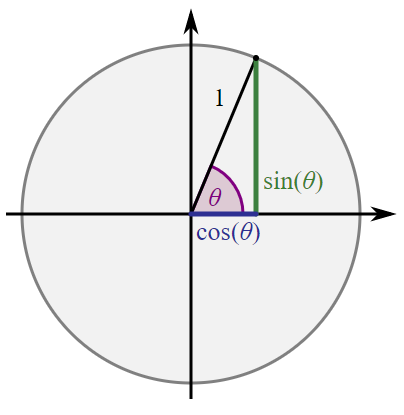
There is an opportunity to connect learning with investigating the constancy of the sine, cosine and tangent ratios for a given angle in right-angled triangles with concepts covered in this topic of study. Refer to Space topic: Pythagoras and Trigonometry.
Teaching and learning summary:
- Revise similar figures and ratio.
- Revise knowledge of Pythagoras’ theorem.
- Revise knowledge of trigonometry.
- Show how to apply Pythagoras’ theorem, trigonometry and scale factors to solve simple and authentic problems.
Students:
- use the correct trigonometrical ratio to solve problems involving the length of sides
- apply knowledge of scale factor and similar figures to solve simple problems
- apply knowledge of trigonometry to solve simple problems
- communicate their thinking, reasoning and solutions.
Some students may:
- assume a diagram is to scale and make assumptions based on this.
- believe that corresponding sides are ‘matching’ regardless of the orientation of the shape. In identifying corresponding sides, it is helpful to ensure the orientation of the shapes is the same, making the corresponding sides easier to identify. The use of concrete materials and dynamic geometry software can assist students to visualise shapes and objects in different orientations. Support students to consider each entire shape when deciding if they are similar.
- not check the scale factor is the same for every side.
- not recognise that a triangle is a right triangle.
- try to use Pythagoras’ theorem with non-right triangles.
- misidentify the trigonometrical ratios to be used.
- apply trigonometrical ratios to non-right triangles.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning about the three trigonometrical ratios.
- We are learning to use the trigonometrical ratios to solve a problem involving the side lengths and angles in a right-angle triangle.
Why are we learning about this?
Trigonometry is the basis of much higher-level mathematics. It is used in many professional areas such as architecture, engineering, aviation, satellite technology and cartography.
What to do
History of trigonometry
- Write down your responses to these questions:
- Where did the idea of trigonometry come from?
- How did it develop?
- Which civilisations were involved?
- The following resource has three articles. View The history of trigonometry: Part 1. Next, view the other two articles: Part 2 and Part 3.
- Write a summary of what you found out with at least three key developments that interested you. Include ways a right-angled triangle was used to measure heights and distances.
Success criteria
- I can identify and label the sides of a right-angled triangle according to a reference angle (θ – hyp, adj, opp).
- I can state the three trigonometrical ratios.
- I can use the trigonometrical ratios to solve a problem involving the side lengths and angles in a right-angled triangle.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Worked examples
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource -
Differentiation
Differentiation involves teachers creating lessons that are accessible and challenging for all students.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Pythagoras’ theorem two ways
In this lesson, students use Pythagoras’ theorem to calculate unknown side lengths in right-angled triangles using algebraic proofs.
Go to resource -
Pythagoras' theorem and trigonometry: short problems
A collection of class problems to allow for varying levels of understanding and application of trigonometry within the classroom.
Go to resource -
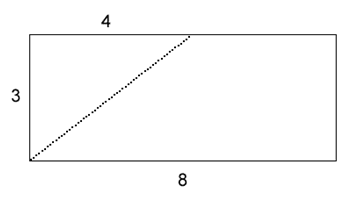
Rectangular arrangement
A simple starter problem requiring students to rearrange shapes within a rectangle to find lengths of sides and perimeter.
Go to resource -
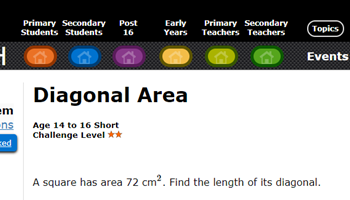
Diagonal area
A more difficult problem requiring students to find the length of the diagonal of a square with only area as the given to work from.
Go to resource -

Pythagoras' theorem
A useful guide on how to teach Pythagoras at a Year 9 level within the subject area of trigonometry. This page contains teaching ideas and gives links to other resources such as dynamic geometric software.
Go to resource
Assessment
By the end of Year 9, students can apply Pythagoras’ theorem and use trigonometric ratios to solve problems involving right-angled triangles.
-

Pythagoras' theorem and trigonometry: short problems
A collection of class problems to allow for varying levels of understanding and application of trigonometry within the classroom.
Go to resource -

Diagonal area
A more difficult problem requiring students to find the length of the diagonal of a square with only area as the given to work from.
Go to resource -

Rectangular arrangement
A simple starter problem requiring students to rearrange shapes within a rectangle to find lengths of sides and perimeter.
Go to resource