Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M8M06
Numeracy Progression: Understanding geometric properties: P7, Understanding units of measurement: P10, Multiplicative strategies: P9
At this level, students are introduced to Pythagoras’ theorem to solve problems involving the side lengths of right-angled triangles.
Students will need an understanding of algebra when using Pythagoras’ theorem. They will need to manipulate equations and substitute values. Students need to be familiar with the formula: c2 = a2 + b2 and understand what the values, a, b and c represent. Students must be able to identify the hypotenuse and to use the rule correctly. They explore this using the theorem in a variety of contexts.
Students should be able to manipulate the formula and recognise that a2 = c2 – b2 can be used to find a shorter side.
Pythagoras’ theorem can be applied to any formula that squares a number. By taking the length of a side to be a variable such as distance, energy, time or even number of people, you can calculate these missing values. In other words, while not related to shapes, if a concept has a formula that squares a number, its variables can be calculated.
Students investigate theorems and conjectures involving triangles. They apply their knowledge of angle facts, triangle congruence, similarity and properties of quadrilaterals to derive results about angles and sides, including Pythagoras’ theorem.
Students learn about Pythagorean triples: (3, 4, 5), (5, 12, 13), (17, 24, 25) and (9, 40, 41), and that they satisfy the condition c2 = a2 + b2, where a, b, and c are the three positive integers. They learn that there is an infinite number of Pythagorean triples.
The concept of Pythagoras‘ theorem will be relevant and useful in following measurement units of study as well as the study of Geography and Design. Students can discuss and compare different applications, demonstrations and proofs of Pythagoras’ theorem.
Teaching and learning summary:
- Revise the types of triangles.
- Revise squaring and taking a square root.
- Introduce Pythagoras’ theorem – why ‘theorem’?
- Investigate right-angled triangles.
- Demonstrate/investigate several proofs.
- Calculate the hypotenuse.
- Show how to use Pythagoras’ theorem to solve simple problems of height.
- Identify Pythagorean triples – (3, 4, 5), (5, 12, 13), (17, 24, 25) and (9, 40, 41).
- Apply rules for finding the perimeter and area of triangles.
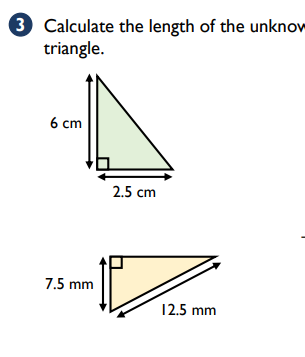
Students:
- identify the hypotenuse in a right-angled triangle, regardless of orientation
- state Pythagoras’ theorem and apply it to finding the length of any side of a right-angled triangle
- demonstrate a proof of Pythagoras’ theorem
- understand what Pythagorean triples are and apply these to tasks
- apply knowledge of the concepts of area, surface area and perimeter
- create equations that describe numbers or relationships.
Some students may:
- not recognise that a triangle is a right triangle.
- try to use Pythagoras’ theorem with non-right triangles.
- not identify correctly which side is the hypotenuse.
- believe that the orientation of the triangle does not matter.
- believe that the shape on each side can only be a square – the theorem holds true for the area of any shape.
- not yet be able to transpose the formula correctly to find a shorter side.
- add all three Pythagorean triples. Giving students images of triangles in different orientations and asking them to identify the sides can develop their visual awareness.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- I can apply my knowledge of Pythagoras' theorem and extend myself with difficult problems.
Why do I need to know this?
Think about all the buildings around you! Think about anything that requires designing, whether it's on paper or with digital software. Pythagoras is all around you.
What to do
For the right-angled triangle below, label the sides (opposite, hypotenuse, adjacent) in relation to the angle marked alpha and write down the trigonometrical ratios.

Success criteria
- I can find the trigonometrical ratios for this tricky right-angled triangle problem.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Worked examples
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Pythagoras investigations and applications
In this lesson students work in small groups to investigate the application of Pythagoras’ theorem to problems in a practical or theoretical context.
Go to resource -

Pythagorean triples
In this lesson students undertake a mathematical exploration to find Pythagorean triples.
Go to resource -
Pythagoras triples
In this task students will investigate Pythagorean triples. The resource includes a lesson plan rubric and sample of student work scored against a rubric.
Go to resource -

How old is the (Pythagorean) theorem?
In this lesson students learn about Pythagoras’ theorem and its application in calculating lengths in right-angled triangles.
Go to resource -

Pythagoras: Cartesian coordinate plane
In this lesson students calculate the distance between any two points on the Cartesian coordinate plane using Pythagoras’ theorem.
Go to resource -
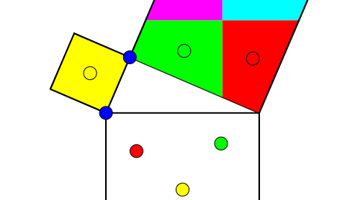
Pythagoras' theorem and Bhaskara
A visual demonstration of Bhaskara’s proof for Pythagoras’ theorem.
Go to resource -
Application of the Pythagorean theorem
In this lesson students are introduced to Pythagorean theorem as a tool to solve application problems.
Go to resource
Assessment
By the end of Year 8, students use Pythagoras’ theorem to solve measurement problems involving unknown lengths of right-angle triangles.
-

Pythagoras triples
In this task students will investigate Pythagorean triples. The resource includes a lesson plan rubric and sample of student work scored against a rubric.
Go to resource -
Pythagoras' problems
A mixed selection of problems to solve using Pythagoras' theorem with accompanying solutions.
Go to resource