Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M10M03
Numeracy Progression: Understanding geometric properties: P7, Understanding units of measurement: P10
At this level, students apply their knowledge of Pythagoras' theorem to solve problems involving angles of elevation and depression and direction. They explore how direction can be indicated using true bearings and compass points.
The use of concrete materials and/or dynamic geometry software can assist students in visualising 3D objects.
Students will use this knowledge in future study when working in three dimensions.
Teaching and learning summary:
- Revise application of Pythagoras’ theorem.
- Revise the trigonometrical ratios.
- Apply knowledge of trigonometrical ratios to find the lengths and angles in contextual problems.

Students will:
- identify the opposite and adjacent sides of a right-angled triangle for a given angle
- state the three trigonometrical ratios
- use the correct trigonometrical ratio to solve a problem involving the side lengths and angles in a right-angle triangle
- use appropriate terminology, diagrams and symbols in mathematical contexts
- select and use the appropriate strategy to solve problems
- provide reasoning to support conclusions that are appropriate to the context
- identify the angle of elevation or depression.
Some students may:
- not appreciate the nature of sine, cosine and tangent – these are ratios, not numbers.
- misidentify the sides of the triangle in relation to the angle given.
- not use the correct trigonometrical ratio and try to apply to non-right-angled triangles.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning how to write a formal proof of a geometric property using the correct mathematical language and notation.
- We are learning how to apply geometrical properties to solve geometry problems.
Why are we learning about this?
- There are many areas where knowledge of shapes and angles is useful.
- It is important that you can communicate your ideas using the correct mathematical terminology and notation.
- If you are going on to study mathematics at a higher level, knowledge of formal proof is important.
What to do
- Angles of elevation and depression
This GeoGebra exercise demonstrates the meaning of ‘angle of elevation’ and ‘angle of depression’. - The spider and the fly
A spider is sitting in the middle of one of the smallest walls in my living room and a fly is resting by the side of the window on the opposite wall, 1.5 m above the ground and 0.5 m from the adjacent wall. The room is 5 m long, 4 m wide and 2.5 m high. What is the shortest distance the spider would have to crawl to catch the fly?To solve this problem, draw a picture (diagram) of the room, labelling the dimensions. What pathways can the spider take?
- How high is the mountain?
Finding the height of an object like a mountain is not as easy as it sounds. The great Adirondack surveyor explains how Verplank Colvin solved this problem in the 1870s using Pythagoras and trigonometry. The methods he devised are still used in surveying today.
Success criteria
- I can identify the opposite and adjacent sides of a right-angled triangle for a given angle.
- I can state the three trigonometrical ratios.
- I can use the correct trigonometrical ratio to solve a problem involving the side lengths and angles in a right-angled triangle.
- I can use appropriate terminology, diagrams and symbols in mathematical contexts.
- I can select and use the appropriate strategy to solve problems.
- I can provide reasoning to support conclusions that are appropriate to the context.
- I can identify the angle of elevation or depression.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Concrete, Representational, Abstract (CRA)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
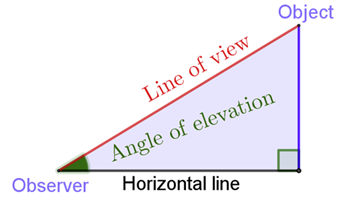
Height and distance
This resource demonstrates the meaning of angles of elevation and depression.
Go to resource -

Angles of elevation and depression
This simple resource gives a visual demonstration of the meaning of elevation and depression.
Go to resource -

The great Adirondack surveyor
This fascinating history of the application of trigonometry to surveying helps students to understand the relevance of the mathematics they are learning.
Go to resource -
Trigonometric trajectories
Use these two engaging real-world contexts to reinforce students’ understanding of trigonometric and Pythagorean relationships.
Go to resource -
Trigonometric function
This module is for teachers who wish to consolidate their content knowledge on the topic of trigonometric functions.
Go to resource -
Solving problems with trigonometry
In this lesson, students apply the concepts of trigonometry to two different situations.
Go to resource -
Right-angled triangles inquiry
This multi-faceted inquiry combines Pythagoras' theorem and trigonometry with algebraic expressions for sequences and area.
Go to resource
Assessment
By the end of Year 10, students can apply Pythagoras’ theorem and trigonometry to solve practical problems involving right-angled triangles.
-

Height and distance
This resource demonstrates the meaning of angles of elevation and depression.
Go to resource -

Angles of elevation and depression
This simple resource gives a visual demonstration of the meaning of elevation and depression.
Go to resource -

The great Adirondack surveyor
This fascinating history of the application of trigonometry to surveying helps students to understand the relevance of the mathematics they are learning.
Go to resource -

Trigonometric trajectories
Use these two engaging real-world contexts to reinforce students’ understanding of trigonometric and Pythagorean relationships.
Go to resource -

Trigonometric function
This module is for teachers who wish to consolidate their content knowledge on the topic of trigonometric functions.
Go to resource -

Solving problems with trigonometry
In this lesson, students apply the concepts of trigonometry to two different situations.
Go to resource -

Right-angled triangles inquiry
This multi-faceted inquiry combines Pythagoras' theorem and trigonometry with algebraic expressions for sequences and area.
Go to resource