Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M8SP04
Numeracy Progression: Understanding geometric properties: P7, Proportional thinking: P6
At this level, students begin to design, create and test algorithms that involve a sequence of steps that identify congruency or similarity of shapes. They describe how algorithms work through classifying and distinguishing between similar and congruent triangles.
Students need to develop their conceptual understanding of congruency. They need to develop the conditions for congruent triangles and use congruent triangles to establish properties of quadrilaterals. They can develop their understanding of what congruency is through visual recognition when generating and matching congruent shapes.
Provide opportunities for students to identify and describe the properties of congruent shapes. Allow students to use different approaches to classify quadrilaterals. If two triangles within the quadrilateral can be shown to be congruent, then the corresponding sides and angles within the triangles will be equal. Classify quadrilaterals by properties of their diagonals – their symmetry and relationships.
Students will learn that if there is a correspondence between the shapes such that corresponding angles and sides are congruent, the shapes are congruent. Have students explore and develop the properties of similarity for triangles using enlargement transformation. Discuss what the term 'similar' means in relation to shapes and specifically to triangles. Discuss the differences between the meaning of 'congruent' and 'similar'.
Use examples of enlargement to explain the notion of scale factor (constant ratio) and similar figures. For example, provide two similar shapes – one twice as big as the other – and have students measure the corresponding angles and ratios of corresponding side lengths to establish the properties of similar figures.
Using their knowledge of congruence triangles and similarity between triangles, students will be able to develop a sorting algorithm and build on their experience with algorithms and flow charts from Year 7 (AC9M7SP04). Have students refine and test their algorithms with class peers. Testing and revaluating is an essential skill when applying algorithmic thinking.
Teachers could ask questions to support student understanding of congruence. For example:
- What patterns, connections and relationships can you see?
- Can you represent or calculate in different ways?
- In what ways can your thinking be generalised?
- What can you infer?
Students need to be immersed in the mathematical language, and understand the terms:
- quadrilateral
- congruent
- transformation
- rotation
- reflect
- translate
- isosceles triangle
- scalene triangle.
Teaching and learning summary:
- Revise algorithms and flowcharts.
- Discuss the concept of a sequence of steps and decision-making.
- Congruent shapes have the same size and shape.
- All pairs of corresponding angles are congruent.
- All pairs of corresponding sides are congruent.
- If shapes have symmetry, there is more than one answer.
- Revise the vocabulary of triangles and quadrilaterals.
- Revise previous knowledge of angles.
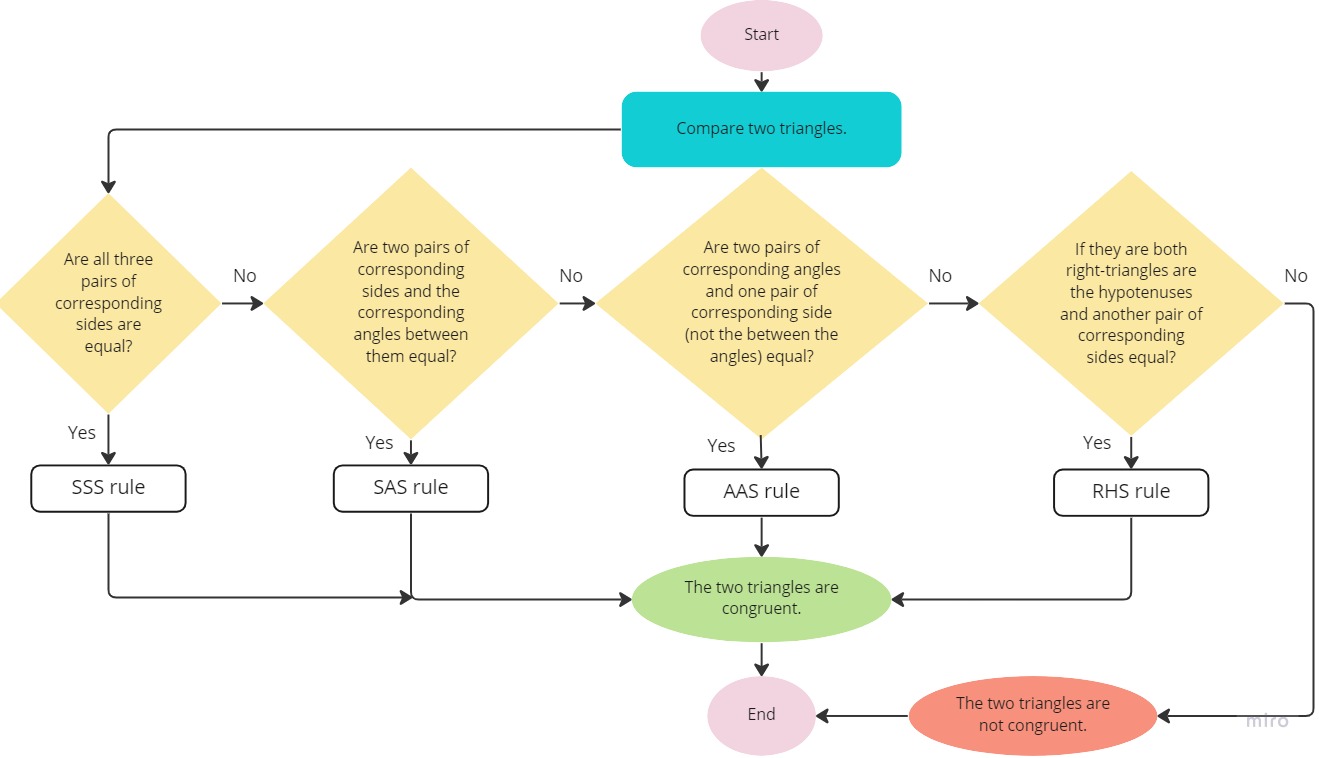
Students:
- can work with flow charts and recall algorithms and sequences from the previous year
- define what congruency means
- can list properties to determine if shapes are similar or congruent
- find the corresponding angles of congruent shapes
- design, create and describe how algorithms work.
Some students may:
- assume that each quadrilateral is distinct, that rectangles cannot be squares, and that once quadrilaterals have four equal sides, they stop being rectangles.
- not understand the properties of each shape when classifying but rather their appearance.
- assume that if more than one triangle can be drawn, then the conditions will specify congruence.
- not label diagrams correctly.
- assume that triangles can be proven congruent using SSA.
- confuse 'similarity' with 'congruence'.
- not show all the steps in a proof and will need a lot of practice in formulating sequenced and logical steps.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- I will identify congruent triangles.
- I will apply the properties to determine if shapes are similar or congruent.
Why are we learning about this?
A reasonable way to think about congruence is to ask ‘How much information do I need to give someone about a figure if they are going to draw it?’ In real-life situations a surveyor may take careful measurements of a landscape. They need to know that everything is important about the landscape from the measurements taken.
What to do
Activity 1: Transformation
This game provides an opportunity to practise transformations to create high scoring triangles.
Transformation Game (maths.org)
Activity 2: Find an unknown angle
This interactive activity allows you to change the shape of the triangle, and work out each line to find the unknown angle.
Finding an unknown angle - Triangle (det.nsw.edu.au)
Success criteria
- I can construct triangles using the conditions for congruence.
- I can list the properties of shapes using congruence and angle properties.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Concrete, Representational, Abstract (CRA)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource -

Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource -

Worked examples
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Geometric reasoning
This teacher resource covers properties of quadrilaterals suitable for the Year 8 student. Task students to create their own steps, sequences or algorithms to recognise, sort and classify them.
Go to resource -
Congruence
This teaching resource gives detailed explanations for testing congruency using worked examples and assessment questions. Students can use the explanations and images to create an infographic or flow chart to classify congruent shapes.
Go to resource -
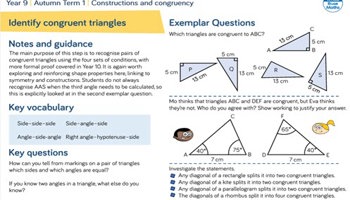
Constructions and congruency
This resource provides guidance, key vocabulary and exemplar questions for constructing triangles, identifying congruent figures and triangles, which all can be used to construct an infographic to sort and classify congruent shapes.
Go to resource
Assessment
By the end of Year 8, student can use algorithms to design, create and test a sequence of steps to make decisions that identify congruency or similarity of shapes. Students can describe their algorithm.
-

Congruence
A teaching resource for teachers and students, with detailed explanations of the curriculum content and worked examples. Have students identify the criteria required to design and create an algorithm that can be used for comparisons between triangles to test for congruency and similarity.
Go to resource -
Congruence Exercises and answers
Engage students by using these exercises on congruence to practise identifying the rules required to design an algorithm that can be successfully used by others. Have students apply this thinking to designing and testing algorithms on triangle congruency.
Go to resource