Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M9SP03
Numeracy Progression: Understanding geometric properties: P7
At this level, students draw on their knowledge of congruency, transformations and ratios of right-angled triangles and apply creativity, critical thinking and reasoning skills to a sequenced geometric problem. For example, students may design a flowchart to prove the congruency between two triangles, or perhaps they create instructions to design a sequenced visual pattern, or use dynamic geometric software to explore three-dimensional (3D) shapes in the x, y, z planes.
An important aspect is to apply algorithmic and computational thinking to their own design, so that the design may be tested and evaluated by others. Encourage students to use real-world scenarios in their design. Perhaps a geometric pattern that can be found in their bedroom rug, for example. Perhaps the 3D shapes are in fact stepped directions a delivery drone must follow. Perhaps finding the shortest distance between landmarks requires a set of directions using Google Maps.
Evaluation and making improvements or refinements is also important. Asking questions of peers and accepting continual feedback helps the task to be more engaging and fun, while cementing important geometric concepts in preparation for more complex thinking with geometry and trigonometry in the later years.
Teaching and learning summary:
- Revise geometry and space topics in relation to congruency, similarity and differences, 2D and 3D representations, and transformations of shapes.
- Revise algorithms and sequence-based computations (AC9M7SP04).
- Model geometric and spatial knowledge to real-world problems.
- Introduce or revise flow-charts and pseudocode.
- Create creative and critical learning opportunities to consolidate knowledge. Collaboration and feedback are appropriate teaching approaches.
Students:
- draw on knowledge of geometric shapes and their properties
- recognise similarities, differences and create patterns in relation to right-angled triangles
- create a real-world problem based on geometric and spatial knowledge and skills
- design and represent sequenced steps and algorithms in order to solve their problem
- evaluate and refine their sequences appropriately based on testing and proofing.
Some students may:
- underestimate how important ‘creativity’ is for creating algorithms with sequenced steps. When roadblocks occur, use the approach of ‘questioning’ students to open up their mind to other possibilities. This will help them to think laterally.
- not realise that there may be several solutions to a problem. Suggest students trial different sequences of steps to find the most effective or efficient pathway. Remind students that there is value in recognising those sequences that lead to incorrect solutions; that is, being aware of incorrect pathways can in fact help ‘debug’ your algorithm.
- underestimate the value of repetitive testing of their sequences to ensure that other users can successfully reach the outcome they intended. Encourage testing and evaluating feedback to refine their algorithm and design.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning to create a series of steps or instructions based on trigonometric ratios.
- We will use our knowledge on geometric constructions and theorems to solve problems.
Why are we learning about this?
You now know that if you can write a set of instructions, you can write an algorithm! We live in a world that is full of simple and complex problems to be solved. With clever algorithms and the immense computing power at our disposal we can tackle large quantities of these problems to make the world better and better. For instance, you are now proficient at using Pythagoras’ theorem and the trigonometric ratios to solve problems involving right-angled triangles. It is common for problems to require us to calculate the length or magnitude of a missing angle or side length. There are several real-world contexts when we would need to do this. Keep reading.
What to do
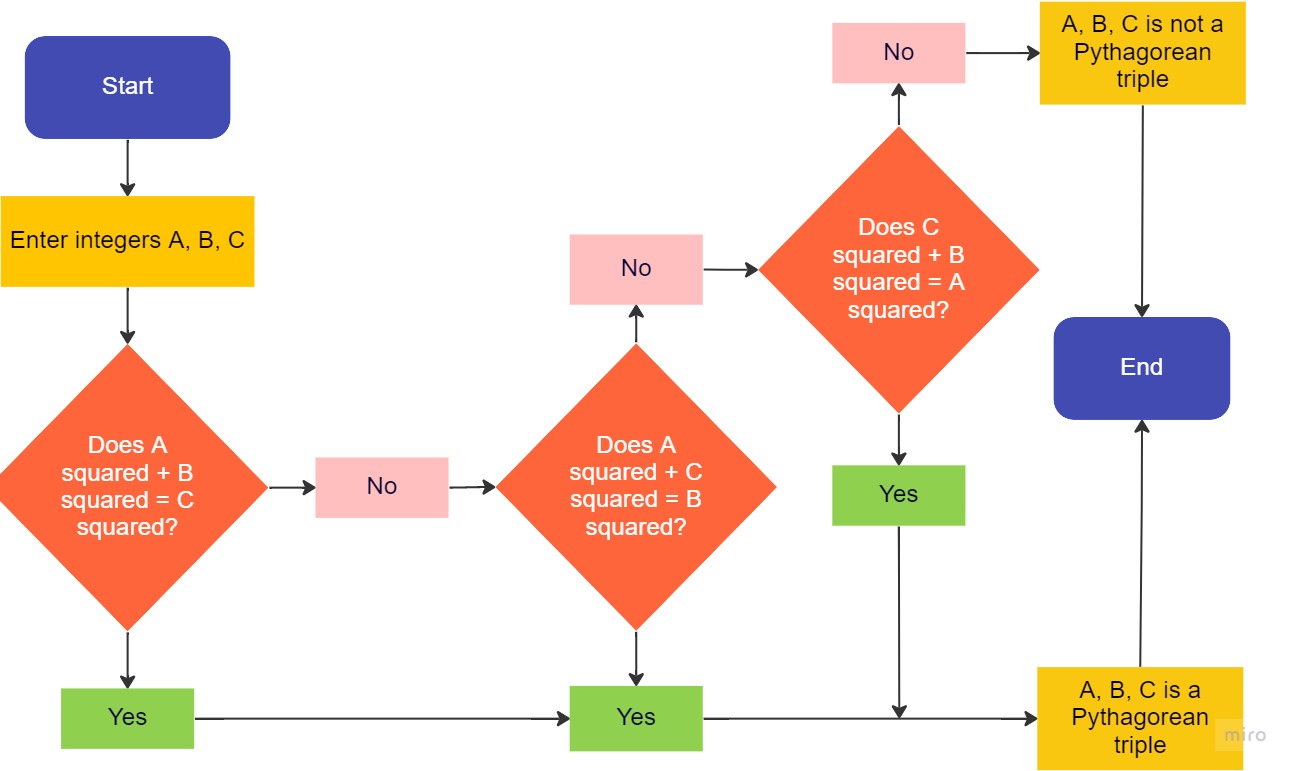
Your task is to produce a set of step-by-step instructions (or a flowchart if you’re keen on a challenge) to guide someone through the solution to one of these problems. The image for this topic on the Planning tool is a wonderful example of a flowchart for determining whether a set of three numbers are a Pythagorean triple. You should consult this image first. You may also choose to use a search engine to browse the many examples of Pythagoras’ theorem and trigonometry flowcharts available. I’ll get you started…
- Identify whether the triangle has a right angle.
- List the known properties of the triangle (for example, 2 side lengths or 1 side length and 1 angle).
- Identify the property that needs to be calculated.
Over to you!
Success criteria
- I can create a series of steps or instructions based on trigonometric ratios.
- I used my knowledge on geometric constructions and theorems to find a way to solve problems that exist in the real world.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-
Classroom talks
Classroom talks enable students to develop language, build mathematical thinking skills and create mathematical meaning through collaborative conversations.
Go to resource -

Collaborative learning
For group work to be effective students need to be taught explicitly how to work together in different settings, such as pairs or larger groups, and they need to practise these skills.
Go to resource -
Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource -
Feedback
It has been shown that good feedback can make a significant difference to a student’s future performance.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Investigating trigonometry ratios
This interactive task evaluates the angles of right-angled triangles by varying the lengths of sides. Using interactives is an efficient way to design sequenced criteria that may be used identify Pythagorean triples or assessing proofs for other geometric theorems.
Go to resource -
Creating triangles
This interactive game engages students with triangle proofs requiring students to use computational thinking to solve the problems. Once successful, students can create an algorithmic infographic or flowchart and have their peers test and provide feedback.
Go to resource
Assessment
By the end of Year 9, students can design, use and test algorithms based on geometric constructions or theorems.
-

Introducing algorithms
Using guidance from the Digital Technologies Hub and your DT department, this resource serves as an appropriate cross-curriculum assessment task. Students use an algorithmic design game to practise building flowcharts and using pseudocode to design and test games or tasks.
Go to resource