Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M7ST03
Numeracy Progression: Interpreting and representing data: P6
At this level, students have been learning about measures of spread in terms of mean, median, mode and range. They use these values to interpret data and data displays. They are familiar with statistical terminology and are ready to conduct their own statistical investigations. However, students will need to be explicitly taught how to structure an investigation. This can be done in four steps:
- Identify a problem – clarify the issue and generate questions that can be answered with the data.
- Collect data – design a plan that will gather the relevant data.
- Analyse data – apply statistical techniques, such as measures of centre and spread.
- Interpret and communicate – select the most appropriate data displays and summarise results in accurate statements.
Guide students to real-world data samples that are meaningful to this age group. Have students either plan and conduct their own independent statistical investigation or provide more scaffolded guidance for the tentative student. Students may need guidance to identify data that is discrete (countable numerical values) and continuous (complex numerical values over a fixed range).
Encourage students to conduct their investigation by hand or by using digital software to create data displays. They should try to show you their independence in analysing and interpreting their data and data display. Provide a structure for their report: Introduction, Data, Analysis and Conclusion.
Students benefit from reporting their results, allowing them to showcase what they have learnt and to engage in classroom talks with their peers.
Teaching and learning summary:
- Revise students’ previous knowledge of mean, median, mode and range.
- Correct any misconceptions they hold before moving forward.
- Have students plan and conduct a statistical investigation involving data for discrete and continuous numerical variables.
- Discuss and demonstrate how to calculate these measures of location with small datasets and larger ones for discrete and continuous variables.
- Demonstrate how to calculate each of these measures from a range of data displays.
- Discuss the usefulness and meaning of each of the measures.
- Use various datasets to illustrate the effect of outliers.
- Use the correct terminology and encourage students to be precise in their use of these terms so that they know the difference between abstract terms.
- Provide opportunity for students to report their findings.

Students:
- know the meaning of the terms 'mean', 'median', 'mode' and 'range'
- plan and conduct their own statistical investigation involving discrete and continuous data
- know which type of data display is appropriate for different datasets
- analyse and interpret distributions of data
- report findings on distribution shape and summary statistics using the correct statistical terminology
- communicate their findings succinctly and accurately
- understand the difference between inference, prediction and speculation.
Some students may:
- confuse the terms 'mean', 'median' and 'mode'.
- not fully appreciate that mean, median and mode are all ‘averages’ (measures of central location) and that the range is a different type of measure (spread).
- not understand that some statistical measures can only be applied to specific types of data.
- have difficulty in finding the mean and median in graphical representation, compared with a table of values.
- struggle to generate their own questions for investigations and may require a set of examples.
- overstate their findings and confuse correlation with causation. Illustrate situations in which these are conflated. For example, as the number of ice creams sold increases, so does the number of sunburnt people; these are both caused by the strength of the sun.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- I am learning how to conduct a statistical investigation using bushfire data.
- I am learning how to analyse data effectively by calculating useful summary statistics, selecting appropriate data displays.
- I will communicate the findings of my statistical investigation.
Why are we learning about this?
Analysing data is key to understanding our world. When something significant happens, it is natural to wonder why. We can theorise about this and offer our own personal explanations. But these are influenced by our own biases and subjectivity. The data tells the true story. Anyone using the same data will calculate the same predictions and, provided they follow appropriate processes, will draw the same conclusions. These skills allow us to separate fact from fiction and get to the bottom of what happened.
What to do
Australia is synonymous with bushfires. Every summer you can expect bushfires somewhere in our southern states. Devastation follows but each year we learn more and that is partly to do with the analysis of the data we collect each year. When we have key information, we make better decisions, provide better advice, provide better resources to control and fight bushfires and so on.
- Investigate the scale of the bushfires that have devastated some of our states.
- Go to the spreadsheet, where you will find data on bushfires in NSW (prescribed burns and wildfires) since 2016. They are organised into separate sheets for you. The data is on the size of the fire, measured in hectares.
- Use the suggestions in the table below to guide your investigation. These originate from the website 100 Years of Bushfire Data, University of NSW.
| Introduction |
|
| Data |
|
| Analysis |
|
| Conclusion |
|
Now that you have been scaffolded through a statistical investigation, could you conduct a statistical investigation alone? Maybe it's about something you're interested in, like why your football team always loses at a particular stadium, or which jobs provide high levels of satisfaction. What data would you need to gather? Which summary statistics will be useful?
The world is your oyster.
Success criteria
- I can conduct a statistical investigation and produce a report.
- I can analyse data effectively by calculating useful summary statistics, selecting appropriate data displays.
- I can communicate the findings of my statistical investigation.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource -

Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource -

Collaborative learning
For group work to be effective students need to be taught explicitly how to work together in different settings, such as pairs or larger groups, and they need to practise these skills.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Sleepy statistics: Part 1
Students conduct a sleep audit over two weeks to test hypotheses regarding improving sleep quality.
Go to resource -
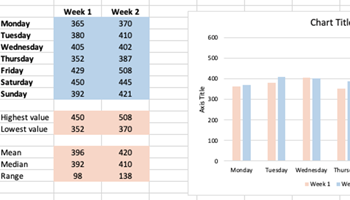
Sleepy statistics: Part 2
In this lesson students conducted a sleep audit over two weeks to test hypotheses regarding improving sleep quality.
Go to resource -
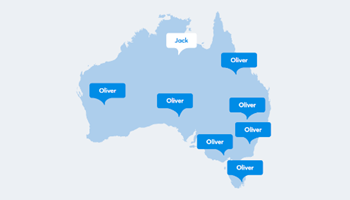
What’s in a name
Students explore the popularity of different birth names by looking at various measures of central tendency such as mean, median and mode. Students also compare and analyse spreadsheet datasets. The resource gives teacher notes, learning intentions and reflection questions for the teacher.
Go to resource -

Representing variability with mean, median, mode and range
In this very detailed lesson plan, students are shown how to calculate summary statistics from a range of graphs and charts. The resource includes student worksheets, teacher notes and presentation material.
Go to resource -
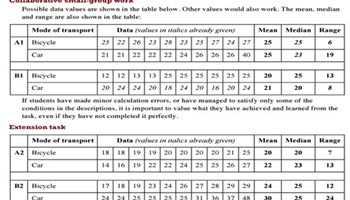
Comparing datasets
A teacher resource designed to expose students to making meaningful comparisons between datasets. The resource includes student worksheets, teacher notes and presentation material. Collaborative learning, class discussion and differentiation opportunities are supported.
Go to resource -
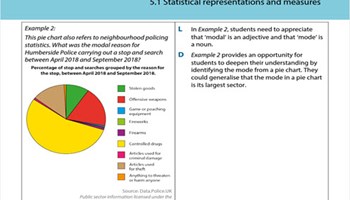
Statistical representations and measures
A teacher-facing article on data displays and summary statistics that provides guidance on key ideas, teacher planning and notes, and common misconceptions students have and how to address them.
Go to resource -

Film ratings: mean and median
This interactive activity demonstrates how using a different statistic (mean or median) to illustrate data, frames and changes your view of the data.
Go to resource
