Expected level of development
Australian Curriculum Mathematics V9: AC9M7N06
Numeracy Progression: Additive strategies: P10, Number and place value: P10, Interpreting fractions: P8, Multiplicative strategies: P10, Proportional thinking: P2
At this level, students are required to use all operations with positive rational numbers and to choose the most appropriate and efficient approach when solving a variety of problems.
It is important for students to have a sound understanding of how to add and subtract rational numbers, particularly fractions and decimals. Essentials concepts to cover are:
- adding and subtracting fractions with common denominators
- multiplying fractions (either with direct multiplication then simplifying the fraction, or with cross-cancelling before multiplying)
- dividing fractions by inverting the second fraction and switching the division to a multiplication (a great way to revise the relationship between multiplication and division as inverse)
- adding and subtracting fractions with unlike denominators (after revising LCM, lowest common multiple).
Manipulatives such as Cuisenaire rods and paper strips are excellent hands-on and visual representations to help make sense of abstract concepts, symbols and algorithms. A useful example is to use rectangle arrays for representing the denominators of fractions.
Develop and consolidate multiplication and division strategies to aid efficient problem-solving with visual and digital tools such as fraction walls, rectangular arrays, algebra tiles, calculators, drawings and gaming. These tools drive engagement and understanding.
Be sure to demonstrate how fractions and percentages can be expressed and manipulated in a variety of formats, depending on the needs of the question. The use of number lines, bar diagrams and concrete materials can help students with their conceptual understanding.
When approaching problems, ask students questions to direct them towards the correct or beneficial representations of rational numbers to choose. For example, ask a student whether it is more appropriate and efficient to use 0.25 rather than 1 2 or 25%. Demonstrate that it’s sometimes easiest to rearrange problems; therefore, knowing the commutative and associative properties, patterning, number facts and place value will build fluency and proficiency.
Solve real-life scenarios to model different approaches to problems. Use questioning and collaboration to recognise different methods, representations and reasonings. Allow students to communicate their estimations, reasonings and ideas.
Teaching and learning summary:
- Build on students’ knowledge of fractions and decimals.
- Extend students’ ability to operate with fractions that have different denominators.
- Demonstrate that numbers can be represented in different ways – relating fractions, decimals and percentages.
- Introduce a variety of methods for operating with fractions, decimals and percentages.
- Encourage the use of estimation so that students can assess if their answer is reasonable.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
We are learning to convert between decimals, fractions and percentages.
Why are we learning about this?
Being able to convert between fractions, decimals and percentages develops our concept of what quantities mean, something we deal with in our everyday life. We use decimals when dealing with money, weight and length, for instance. Percentages are important for understanding financial aspects, and fractions are important as they tell us what portion of a whole we need, have or want.
What to do
Play Decimal, Fraction, Percentage dominoes.
The purpose of this game is to build your own set of mathematical dominoes and challenge people in your house to solve them.
Use the table below to select a range of different values. If you are not confident with conversions yet, use technology to assist. This game will deepen your understanding.
| Decimal | Fraction | Percentage |
| 0.75 | 3 4 | 75% |
| 0.6 | 3 5 | 60% |
| 0.5 | 1 2 | 50% |
| 0.45 | 9 20 | 45% |
Now it’s your turn!
Now use these templates to build your dominos. You could do it by hand or with a device. You can only use two representations of each number. Mix it up. You can’t have two representations of the same number on the same domino.
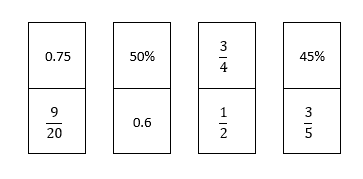
Once you’ve made a stack of dominos (at least 10) you can challenge people to try and place them down correctly, so that every join has two representations of the same number. Keep track of how fast each person does it and crown the champion! I bet it will be you.
Success criteria
I can efficiently convert between fractions, decimals and percentages.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-
Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -
Concrete, Representational, Abstract (CRA model)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -
Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource -
Using games and storybooks
Games and storybooks are great resources to use in the classroom and are engaging for students.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
Estimating and rounding decimals
In this lesson, students draw on prior knowledge of rounding whole numbers.
Go to resource -
Patterns, rules and graphs
In this lesson, students use games to learn about space and location on a Cartesian plane.
Go to resource -
Practical numbers: Part 2
In this lesson we use the context of an ancient bazaar to investigate measurement systems.
Go to resource -
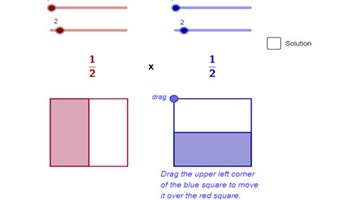
Multiplying fractions
This interactive resource allows students to visually follow the multiplication of fractions using area models.
Go to resource -
Percentage of an amount
This interactive resource uses number lines to show students how to find the percentage of an amount.
Go to resource -
Percentages
This module is for teachers who wish to consolidate their content knowledge on the topic of percentages. It looks at writing percentages as decimals and fractions, finding the percentage of a quantity and operating with percentages.
Go to resource -
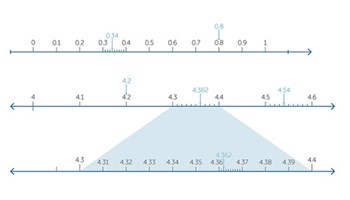
Decimals and percentages
This module uses a number line for whole numbers and fractions to understand place value.
Go to resource